Differentiation¶
Numerical derivatives (diff, diffs)¶
- mpmath.diff(ctx, f, x, n=1, **options)¶
Numerically computes the derivative of
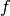 ,
, 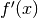 , or generally for
an integer
, or generally for
an integer 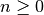 , the
, the  -th derivative
-th derivative 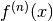 .
A few basic examples are:
.
A few basic examples are:>>> from mpmath import * >>> mp.dps = 15; mp.pretty = True >>> diff(lambda x: x**2 + x, 1.0) 3.0 >>> diff(lambda x: x**2 + x, 1.0, 2) 2.0 >>> diff(lambda x: x**2 + x, 1.0, 3) 0.0 >>> nprint([diff(exp, 3, n) for n in range(5)]) # exp'(x) = exp(x) [20.0855, 20.0855, 20.0855, 20.0855, 20.0855]
Even more generally, given a tuple of arguments
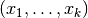 and order
and order 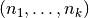 , the partial derivative
, the partial derivative
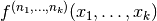 is evaluated. For example:
is evaluated. For example:>>> diff(lambda x,y: 3*x*y + 2*y - x, (0.25, 0.5), (0,1)) 2.75 >>> diff(lambda x,y: 3*x*y + 2*y - x, (0.25, 0.5), (1,1)) 3.0
Options
The following optional keyword arguments are recognized:
- method
- Supported methods are 'step' or 'quad': derivatives may be
computed using either a finite difference with a small step
size
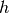 (default), or numerical quadrature.
(default), or numerical quadrature. - direction
- Direction of finite difference: can be -1 for a left difference, 0 for a central difference (default), or +1 for a right difference; more generally can be any complex number.
- addprec
- Extra precision for
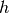 used to account for the function’s
sensitivity to perturbations (default = 10).
used to account for the function’s
sensitivity to perturbations (default = 10). - relative
- Choose
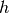 relative to the magnitude of
relative to the magnitude of 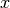 , rather than an
absolute value; useful for large or tiny
, rather than an
absolute value; useful for large or tiny 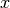 (default = False).
(default = False). - h
- As an alternative to addprec and relative, manually
select the step size
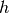 .
. - singular
- If True, evaluation exactly at the point
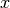 is avoided; this is
useful for differentiating functions with removable singularities.
Default = False.
is avoided; this is
useful for differentiating functions with removable singularities.
Default = False. - radius
- Radius of integration contour (with method = 'quad').
Default = 0.25. A larger radius typically is faster and more
accurate, but it must be chosen so that
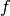 has no
singularities within the radius from the evaluation point.
has no
singularities within the radius from the evaluation point.
A finite difference requires
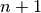 function evaluations and must be
performed at
function evaluations and must be
performed at 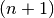 times the target precision. Accordingly,
times the target precision. Accordingly, 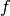 must
support fast evaluation at high precision.
must
support fast evaluation at high precision.With integration, a larger number of function evaluations is required, but not much extra precision is required. For high order derivatives, this method may thus be faster if f is very expensive to evaluate at high precision.
Further examples
The direction option is useful for computing left- or right-sided derivatives of nonsmooth functions:
>>> diff(abs, 0, direction=0) 0.0 >>> diff(abs, 0, direction=1) 1.0 >>> diff(abs, 0, direction=-1) -1.0
More generally, if the direction is nonzero, a right difference is computed where the step size is multiplied by sign(direction). For example, with direction=+j, the derivative from the positive imaginary direction will be computed:
>>> diff(abs, 0, direction=j) (0.0 - 1.0j)
With integration, the result may have a small imaginary part even even if the result is purely real:
>>> diff(sqrt, 1, method='quad') (0.5 - 4.59...e-26j) >>> chop(_) 0.5
Adding precision to obtain an accurate value:
>>> diff(cos, 1e-30) 0.0 >>> diff(cos, 1e-30, h=0.0001) -9.99999998328279e-31 >>> diff(cos, 1e-30, addprec=100) -1.0e-30
- mpmath.diffs(ctx, f, x, n=None, **options)¶
Returns a generator that yields the sequence of derivatives
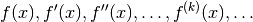
With method='step', diffs() uses only
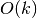 function evaluations to generate the first
function evaluations to generate the first 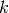 derivatives,
rather than the roughly
derivatives,
rather than the roughly 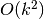 evaluations
required if one calls diff()
evaluations
required if one calls diff() 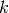 separate times.
separate times.With
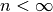 , the generator stops as soon as the
, the generator stops as soon as the
 -th derivative has been generated. If the exact number of
needed derivatives is known in advance, this is further
slightly more efficient.
-th derivative has been generated. If the exact number of
needed derivatives is known in advance, this is further
slightly more efficient.Options are the same as for diff().
Examples
>>> from mpmath import * >>> mp.dps = 15 >>> nprint(list(diffs(cos, 1, 5))) [0.540302, -0.841471, -0.540302, 0.841471, 0.540302, -0.841471] >>> for i, d in zip(range(6), diffs(cos, 1)): ... print("%s %s" % (i, d)) ... 0 0.54030230586814 1 -0.841470984807897 2 -0.54030230586814 3 0.841470984807897 4 0.54030230586814 5 -0.841470984807897
Composition of derivatives (diffs_prod, diffs_exp)¶
- mpmath.diffs_prod(ctx, factors)¶
Given a list of
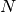 iterables or generators yielding
iterables or generators yielding
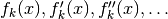 for
for 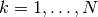 ,
generate
,
generate 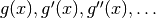 where
where
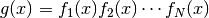 .
.At high precision and for large orders, this is typically more efficient than numerical differentiation if the derivatives of each
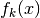 admit direct computation.
admit direct computation.Note: This function does not increase the working precision internally, so guard digits may have to be added externally for full accuracy.
Examples
>>> from mpmath import * >>> mp.dps = 15; mp.pretty = True >>> f = lambda x: exp(x)*cos(x)*sin(x) >>> u = diffs(f, 1) >>> v = mp.diffs_prod([diffs(exp,1), diffs(cos,1), diffs(sin,1)]) >>> next(u); next(v) 1.23586333600241 1.23586333600241 >>> next(u); next(v) 0.104658952245596 0.104658952245596 >>> next(u); next(v) -5.96999877552086 -5.96999877552086 >>> next(u); next(v) -12.4632923122697 -12.4632923122697
- mpmath.diffs_exp(ctx, fdiffs)¶
Given an iterable or generator yielding
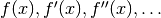 generate
generate 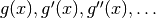 where
where 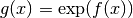 .
.At high precision and for large orders, this is typically more efficient than numerical differentiation if the derivatives of
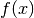 admit direct computation.
admit direct computation.Note: This function does not increase the working precision internally, so guard digits may have to be added externally for full accuracy.
Examples
The derivatives of the gamma function can be computed using logarithmic differentiation:
>>> from mpmath import * >>> mp.dps = 15; mp.pretty = True >>> >>> def diffs_loggamma(x): ... yield loggamma(x) ... i = 0 ... while 1: ... yield psi(i,x) ... i += 1 ... >>> u = diffs_exp(diffs_loggamma(3)) >>> v = diffs(gamma, 3) >>> next(u); next(v) 2.0 2.0 >>> next(u); next(v) 1.84556867019693 1.84556867019693 >>> next(u); next(v) 2.49292999190269 2.49292999190269 >>> next(u); next(v) 3.44996501352367 3.44996501352367
Fractional derivatives / differintegration (differint)¶
- mpmath.differint(ctx, f, x, n=1, x0=0)¶
Calculates the Riemann-Liouville differintegral, or fractional derivative, defined by
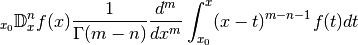
where
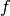 is a given (presumably well-behaved) function,
is a given (presumably well-behaved) function,
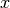 is the evaluation point,
is the evaluation point,  is the order, and
is the order, and 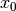 is
the reference point of integration (
is
the reference point of integration (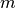 is an arbitrary
parameter selected automatically).
is an arbitrary
parameter selected automatically).With
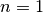 , this is just the standard derivative
, this is just the standard derivative 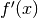 ; with
; with 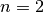 ,
the second derivative
,
the second derivative 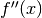 , etc. With
, etc. With 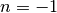 , it gives
, it gives
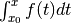 , with
, with 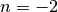 it gives
it gives 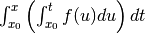 , etc.
, etc.As
 is permitted to be any number, this operator generalizes
iterated differentiation and iterated integration to a single
operator with a continuous order parameter.
is permitted to be any number, this operator generalizes
iterated differentiation and iterated integration to a single
operator with a continuous order parameter.Examples
There is an exact formula for the fractional derivative of a monomial
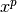 , which may be used as a reference. For example,
the following gives a half-derivative (order 0.5):
, which may be used as a reference. For example,
the following gives a half-derivative (order 0.5):>>> from mpmath import * >>> mp.dps = 15; mp.pretty = True >>> x = mpf(3); p = 2; n = 0.5 >>> differint(lambda t: t**p, x, n) 7.81764019044672 >>> gamma(p+1)/gamma(p-n+1) * x**(p-n) 7.81764019044672
Another useful test function is the exponential function, whose integration / differentiation formula easy generalizes to arbitrary order. Here we first compute a third derivative, and then a triply nested integral. (The reference point
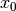 is set to
is set to 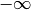 to avoid nonzero endpoint terms.):
to avoid nonzero endpoint terms.):>>> differint(lambda x: exp(pi*x), -1.5, 3) 0.278538406900792 >>> exp(pi*-1.5) * pi**3 0.278538406900792 >>> differint(lambda x: exp(pi*x), 3.5, -3, -inf) 1922.50563031149 >>> exp(pi*3.5) / pi**3 1922.50563031149
However, for noninteger
 , the differentiation formula for the
exponential function must be modified to give the same result as the
Riemann-Liouville differintegral:
, the differentiation formula for the
exponential function must be modified to give the same result as the
Riemann-Liouville differintegral:>>> x = mpf(3.5) >>> c = pi >>> n = 1+2*j >>> differint(lambda x: exp(c*x), x, n) (-123295.005390743 + 140955.117867654j) >>> x**(-n) * exp(c)**x * (x*c)**n * gammainc(-n, 0, x*c) / gamma(-n) (-123295.005390743 + 140955.117867654j)