Bessel functions and related functions¶
The functions in this section arise as solutions to various differential equations in physics, typically describing wavelike oscillatory behavior or a combination of oscillation and exponential decay or growth. Mathematically, they are special cases of the confluent hypergeometric functions \(\,_0F_1\), \(\,_1F_1\) and \(\,_1F_2\) (see Hypergeometric functions).
Bessel functions¶
besselj()¶
- mpmath.besselj(n, x, derivative=0)¶
besselj(n, x, derivative=0)gives the Bessel function of the first kind \(J_n(x)\). Bessel functions of the first kind are defined as solutions of the differential equation\[x^2 y'' + x y' + (x^2 - n^2) y = 0\]which appears, among other things, when solving the radial part of Laplace’s equation in cylindrical coordinates. This equation has two solutions for given \(n\), where the \(J_n\)-function is the solution that is nonsingular at \(x = 0\). For positive integer \(n\), \(J_n(x)\) behaves roughly like a sine (odd \(n\)) or cosine (even \(n\)) multiplied by a magnitude factor that decays slowly as \(x \to \pm\infty\).
Generally, \(J_n\) is a special case of the hypergeometric function \(\,_0F_1\):
\[J_n(x) = \frac{x^n}{2^n \Gamma(n+1)} \,_0F_1\left(n+1,-\frac{x^2}{4}\right)\]With derivative = \(m \ne 0\), the \(m\)-th derivative
\[\frac{d^m}{dx^m} J_n(x)\]is computed.
Plots
# Bessel function J_n(x) on the real line for n=0,1,2,3 j0 = lambda x: besselj(0,x) j1 = lambda x: besselj(1,x) j2 = lambda x: besselj(2,x) j3 = lambda x: besselj(3,x) plot([j0,j1,j2,j3],[0,14])
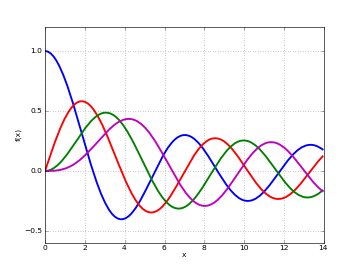
# Bessel function J_n(z) in the complex plane cplot(lambda z: besselj(1,z), [-8,8], [-8,8], points=50000)
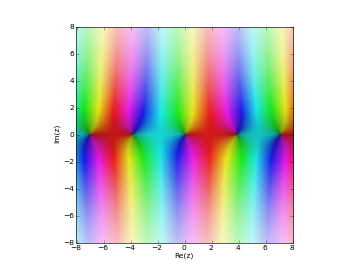
Examples
Evaluation is supported for arbitrary arguments, and at arbitrary precision:
>>> from mpmath import * >>> mp.dps = 15; mp.pretty = True >>> besselj(2, 1000) -0.024777229528606 >>> besselj(4, 0.75) 0.000801070086542314 >>> besselj(2, 1000j) (-2.48071721019185e+432 + 6.41567059811949e-437j) >>> mp.dps = 25 >>> besselj(0.75j, 3+4j) (-2.778118364828153309919653 - 1.5863603889018621585533j) >>> mp.dps = 50 >>> besselj(1, pi) 0.28461534317975275734531059968613140570981118184947
Arguments may be large:
>>> mp.dps = 25 >>> besselj(0, 10000) -0.007096160353388801477265164 >>> besselj(0, 10**10) 0.000002175591750246891726859055 >>> besselj(2, 10**100) 7.337048736538615712436929e-51 >>> besselj(2, 10**5*j) (-3.540725411970948860173735e+43426 + 4.4949812409615803110051e-43433j)
The Bessel functions of the first kind satisfy simple symmetries around \(x = 0\):
>>> mp.dps = 15 >>> nprint([besselj(n,0) for n in range(5)]) [1.0, 0.0, 0.0, 0.0, 0.0] >>> nprint([besselj(n,pi) for n in range(5)]) [-0.304242, 0.284615, 0.485434, 0.333458, 0.151425] >>> nprint([besselj(n,-pi) for n in range(5)]) [-0.304242, -0.284615, 0.485434, -0.333458, 0.151425]
Roots of Bessel functions are often used:
>>> nprint([findroot(j0, k) for k in [2, 5, 8, 11, 14]]) [2.40483, 5.52008, 8.65373, 11.7915, 14.9309] >>> nprint([findroot(j1, k) for k in [3, 7, 10, 13, 16]]) [3.83171, 7.01559, 10.1735, 13.3237, 16.4706]
The roots are not periodic, but the distance between successive roots asymptotically approaches \(2 \pi\). Bessel functions of the first kind have the following normalization:
>>> quadosc(j0, [0, inf], period=2*pi) 1.0 >>> quadosc(j1, [0, inf], period=2*pi) 1.0
For \(n = 1/2\) or \(n = -1/2\), the Bessel function reduces to a trigonometric function:
>>> x = 10 >>> besselj(0.5, x), sqrt(2/(pi*x))*sin(x) (-0.13726373575505, -0.13726373575505) >>> besselj(-0.5, x), sqrt(2/(pi*x))*cos(x) (-0.211708866331398, -0.211708866331398)
Derivatives of any order can be computed (negative orders correspond to integration):
>>> mp.dps = 25 >>> besselj(0, 7.5, 1) -0.1352484275797055051822405 >>> diff(lambda x: besselj(0,x), 7.5) -0.1352484275797055051822405 >>> besselj(0, 7.5, 10) -0.1377811164763244890135677 >>> diff(lambda x: besselj(0,x), 7.5, 10) -0.1377811164763244890135677 >>> besselj(0,7.5,-1) - besselj(0,3.5,-1) -0.1241343240399987693521378 >>> quad(j0, [3.5, 7.5]) -0.1241343240399987693521378
Differentiation with a noninteger order gives the fractional derivative in the sense of the Riemann-Liouville differintegral, as computed by
differint():>>> mp.dps = 15 >>> besselj(1, 3.5, 0.75) -0.385977722939384 >>> differint(lambda x: besselj(1, x), 3.5, 0.75) -0.385977722939384
bessely()¶
- mpmath.bessely(n, x, derivative=0)¶
bessely(n, x, derivative=0)gives the Bessel function of the second kind,\[Y_n(x) = \frac{J_n(x) \cos(\pi n) - J_{-n}(x)}{\sin(\pi n)}.\]For \(n\) an integer, this formula should be understood as a limit. With derivative = \(m \ne 0\), the \(m\)-th derivative
\[\frac{d^m}{dx^m} Y_n(x)\]is computed.
Plots
# Bessel function of 2nd kind Y_n(x) on the real line for n=0,1,2,3 y0 = lambda x: bessely(0,x) y1 = lambda x: bessely(1,x) y2 = lambda x: bessely(2,x) y3 = lambda x: bessely(3,x) plot([y0,y1,y2,y3],[0,10],[-4,1])
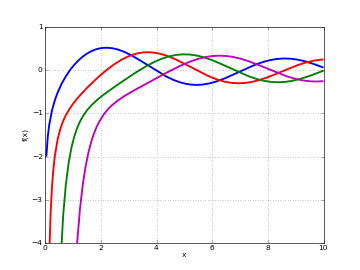
# Bessel function of 2nd kind Y_n(z) in the complex plane cplot(lambda z: bessely(1,z), [-8,8], [-8,8], points=50000)
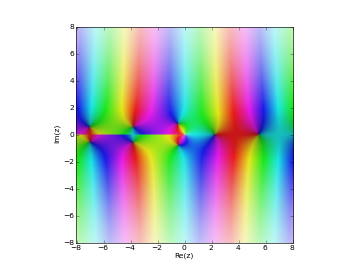
Examples
Some values of \(Y_n(x)\):
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> bessely(0,0), bessely(1,0), bessely(2,0) (-inf, -inf, -inf) >>> bessely(1, pi) 0.3588729167767189594679827 >>> bessely(0.5, 3+4j) (9.242861436961450520325216 - 3.085042824915332562522402j)
Arguments may be large:
>>> bessely(0, 10000) 0.00364780555898660588668872 >>> bessely(2.5, 10**50) -4.8952500412050989295774e-26 >>> bessely(2.5, -10**50) (0.0 + 4.8952500412050989295774e-26j)
Derivatives and antiderivatives of any order can be computed:
>>> bessely(2, 3.5, 1) 0.3842618820422660066089231 >>> diff(lambda x: bessely(2, x), 3.5) 0.3842618820422660066089231 >>> bessely(0.5, 3.5, 1) -0.2066598304156764337900417 >>> diff(lambda x: bessely(0.5, x), 3.5) -0.2066598304156764337900417 >>> diff(lambda x: bessely(2, x), 0.5, 10) -208173867409.5547350101511 >>> bessely(2, 0.5, 10) -208173867409.5547350101511 >>> bessely(2, 100.5, 100) 0.02668487547301372334849043 >>> quad(lambda x: bessely(2,x), [1,3]) -1.377046859093181969213262 >>> bessely(2,3,-1) - bessely(2,1,-1) -1.377046859093181969213262
besseli()¶
- mpmath.besseli(n, x, derivative=0)¶
besseli(n, x, derivative=0)gives the modified Bessel function of the first kind,\[I_n(x) = i^{-n} J_n(ix).\]With derivative = \(m \ne 0\), the \(m\)-th derivative
\[\frac{d^m}{dx^m} I_n(x)\]is computed.
Plots
# Modified Bessel function I_n(x) on the real line for n=0,1,2,3 i0 = lambda x: besseli(0,x) i1 = lambda x: besseli(1,x) i2 = lambda x: besseli(2,x) i3 = lambda x: besseli(3,x) plot([i0,i1,i2,i3],[0,5],[0,5])
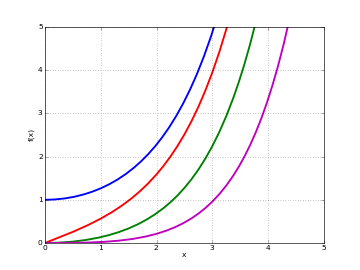
# Modified Bessel function I_n(z) in the complex plane cplot(lambda z: besseli(1,z), [-8,8], [-8,8], points=50000)
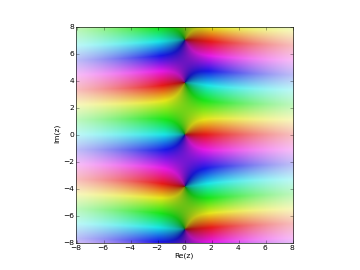
Examples
Some values of \(I_n(x)\):
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> besseli(0,0) 1.0 >>> besseli(1,0) 0.0 >>> besseli(0,1) 1.266065877752008335598245 >>> besseli(3.5, 2+3j) (-0.2904369752642538144289025 - 0.4469098397654815837307006j)
Arguments may be large:
>>> besseli(2, 1000) 2.480717210191852440616782e+432 >>> besseli(2, 10**10) 4.299602851624027900335391e+4342944813 >>> besseli(2, 6000+10000j) (-2.114650753239580827144204e+2603 + 4.385040221241629041351886e+2602j)
For integers \(n\), the following integral representation holds:
>>> mp.dps = 15 >>> n = 3 >>> x = 2.3 >>> quad(lambda t: exp(x*cos(t))*cos(n*t), [0,pi])/pi 0.349223221159309 >>> besseli(n,x) 0.349223221159309
Derivatives and antiderivatives of any order can be computed:
>>> mp.dps = 25 >>> besseli(2, 7.5, 1) 195.8229038931399062565883 >>> diff(lambda x: besseli(2,x), 7.5) 195.8229038931399062565883 >>> besseli(2, 7.5, 10) 153.3296508971734525525176 >>> diff(lambda x: besseli(2,x), 7.5, 10) 153.3296508971734525525176 >>> besseli(2,7.5,-1) - besseli(2,3.5,-1) 202.5043900051930141956876 >>> quad(lambda x: besseli(2,x), [3.5, 7.5]) 202.5043900051930141956876
besselk()¶
- mpmath.besselk(n, x)¶
besselk(n, x)gives the modified Bessel function of the second kind,\[K_n(x) = \frac{\pi}{2} \frac{I_{-n}(x)-I_{n}(x)}{\sin(\pi n)}\]For \(n\) an integer, this formula should be understood as a limit.
Plots
# Modified Bessel function of 2nd kind K_n(x) on the real line for n=0,1,2,3 k0 = lambda x: besselk(0,x) k1 = lambda x: besselk(1,x) k2 = lambda x: besselk(2,x) k3 = lambda x: besselk(3,x) plot([k0,k1,k2,k3],[0,8],[0,5])
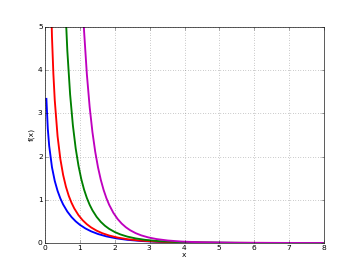
# Modified Bessel function of 2nd kind K_n(z) in the complex plane cplot(lambda z: besselk(1,z), [-8,8], [-8,8], points=50000)
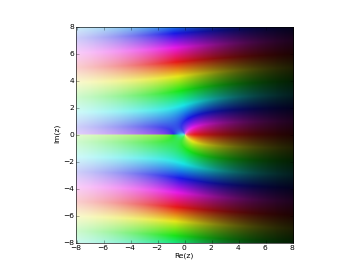
Examples
Evaluation is supported for arbitrary complex arguments:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> besselk(0,1) 0.4210244382407083333356274 >>> besselk(0, -1) (0.4210244382407083333356274 - 3.97746326050642263725661j) >>> besselk(3.5, 2+3j) (-0.02090732889633760668464128 + 0.2464022641351420167819697j) >>> besselk(2+3j, 0.5) (0.9615816021726349402626083 + 0.1918250181801757416908224j)
Arguments may be large:
>>> besselk(0, 100) 4.656628229175902018939005e-45 >>> besselk(1, 10**6) 4.131967049321725588398296e-434298 >>> besselk(1, 10**6*j) (0.001140348428252385844876706 - 0.0005200017201681152909000961j) >>> besselk(4.5, fmul(10**50, j, exact=True)) (1.561034538142413947789221e-26 + 1.243554598118700063281496e-25j)
The point \(x = 0\) is a singularity (logarithmic if \(n = 0\)):
>>> besselk(0,0) +inf >>> besselk(1,0) +inf >>> for n in range(-4, 5): ... print(besselk(n, '1e-1000')) ... 4.8e+4001 8.0e+3000 2.0e+2000 1.0e+1000 2302.701024509704096466802 1.0e+1000 2.0e+2000 8.0e+3000 4.8e+4001
Bessel function zeros¶
besseljzero()¶
- mpmath.besseljzero(v, m, derivative=0)¶
For a real order \(\nu \ge 0\) and a positive integer \(m\), returns \(j_{\nu,m}\), the \(m\)-th positive zero of the Bessel function of the first kind \(J_{\nu}(z)\) (see
besselj()). Alternatively, with derivative=1, gives the first nonnegative simple zero \(j'_{\nu,m}\) of \(J'_{\nu}(z)\).The indexing convention is that used by Abramowitz & Stegun and the DLMF. Note the special case \(j'_{0,1} = 0\), while all other zeros are positive. In effect, only simple zeros are counted (all zeros of Bessel functions are simple except possibly \(z = 0\)) and \(j_{\nu,m}\) becomes a monotonic function of both \(\nu\) and \(m\).
The zeros are interlaced according to the inequalities
\[ \begin{align}\begin{aligned}j'_{\nu,k} < j_{\nu,k} < j'_{\nu,k+1}\\j_{\nu,1} < j_{\nu+1,2} < j_{\nu,2} < j_{\nu+1,2} < j_{\nu,3} < \cdots\end{aligned}\end{align} \]Examples
Initial zeros of the Bessel functions \(J_0(z), J_1(z), J_2(z)\):
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> besseljzero(0,1); besseljzero(0,2); besseljzero(0,3) 2.404825557695772768621632 5.520078110286310649596604 8.653727912911012216954199 >>> besseljzero(1,1); besseljzero(1,2); besseljzero(1,3) 3.831705970207512315614436 7.01558666981561875353705 10.17346813506272207718571 >>> besseljzero(2,1); besseljzero(2,2); besseljzero(2,3) 5.135622301840682556301402 8.417244140399864857783614 11.61984117214905942709415
Initial zeros of \(J'_0(z), J'_1(z), J'_2(z)\):
0.0 3.831705970207512315614436 7.01558666981561875353705 >>> besseljzero(1,1,1); besseljzero(1,2,1); besseljzero(1,3,1) 1.84118378134065930264363 5.331442773525032636884016 8.536316366346285834358961 >>> besseljzero(2,1,1); besseljzero(2,2,1); besseljzero(2,3,1) 3.054236928227140322755932 6.706133194158459146634394 9.969467823087595793179143
Zeros with large index:
>>> besseljzero(0,100); besseljzero(0,1000); besseljzero(0,10000) 313.3742660775278447196902 3140.807295225078628895545 31415.14114171350798533666 >>> besseljzero(5,100); besseljzero(5,1000); besseljzero(5,10000) 321.1893195676003157339222 3148.657306813047523500494 31422.9947255486291798943 >>> besseljzero(0,100,1); besseljzero(0,1000,1); besseljzero(0,10000,1) 311.8018681873704508125112 3139.236339643802482833973 31413.57032947022399485808
Zeros of functions with large order:
>>> besseljzero(50,1) 57.11689916011917411936228 >>> besseljzero(50,2) 62.80769876483536093435393 >>> besseljzero(50,100) 388.6936600656058834640981 >>> besseljzero(50,1,1) 52.99764038731665010944037 >>> besseljzero(50,2,1) 60.02631933279942589882363 >>> besseljzero(50,100,1) 387.1083151608726181086283
Zeros of functions with fractional order:
>>> besseljzero(0.5,1); besseljzero(1.5,1); besseljzero(2.25,4) 3.141592653589793238462643 4.493409457909064175307881 15.15657692957458622921634
Both \(J_{\nu}(z)\) and \(J'_{\nu}(z)\) can be expressed as infinite products over their zeros:
>>> v,z = 2, mpf(1) >>> (z/2)**v/gamma(v+1) * \ ... nprod(lambda k: 1-(z/besseljzero(v,k))**2, [1,inf]) ... 0.1149034849319004804696469 >>> besselj(v,z) 0.1149034849319004804696469 >>> (z/2)**(v-1)/2/gamma(v) * \ ... nprod(lambda k: 1-(z/besseljzero(v,k,1))**2, [1,inf]) ... 0.2102436158811325550203884 >>> besselj(v,z,1) 0.2102436158811325550203884
besselyzero()¶
- mpmath.besselyzero(v, m, derivative=0)¶
For a real order \(\nu \ge 0\) and a positive integer \(m\), returns \(y_{\nu,m}\), the \(m\)-th positive zero of the Bessel function of the second kind \(Y_{\nu}(z)\) (see
bessely()). Alternatively, with derivative=1, gives the first positive zero \(y'_{\nu,m}\) of \(Y'_{\nu}(z)\).The zeros are interlaced according to the inequalities
\[ \begin{align}\begin{aligned}y_{\nu,k} < y'_{\nu,k} < y_{\nu,k+1}\\y_{\nu,1} < y_{\nu+1,2} < y_{\nu,2} < y_{\nu+1,2} < y_{\nu,3} < \cdots\end{aligned}\end{align} \]Examples
Initial zeros of the Bessel functions \(Y_0(z), Y_1(z), Y_2(z)\):
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> besselyzero(0,1); besselyzero(0,2); besselyzero(0,3) 0.8935769662791675215848871 3.957678419314857868375677 7.086051060301772697623625 >>> besselyzero(1,1); besselyzero(1,2); besselyzero(1,3) 2.197141326031017035149034 5.429681040794135132772005 8.596005868331168926429606 >>> besselyzero(2,1); besselyzero(2,2); besselyzero(2,3) 3.384241767149593472701426 6.793807513268267538291167 10.02347797936003797850539
Initial zeros of \(Y'_0(z), Y'_1(z), Y'_2(z)\):
>>> besselyzero(0,1,1); besselyzero(0,2,1); besselyzero(0,3,1) 2.197141326031017035149034 5.429681040794135132772005 8.596005868331168926429606 >>> besselyzero(1,1,1); besselyzero(1,2,1); besselyzero(1,3,1) 3.683022856585177699898967 6.941499953654175655751944 10.12340465543661307978775 >>> besselyzero(2,1,1); besselyzero(2,2,1); besselyzero(2,3,1) 5.002582931446063945200176 8.350724701413079526349714 11.57419546521764654624265
Zeros with large index:
>>> besselyzero(0,100); besselyzero(0,1000); besselyzero(0,10000) 311.8034717601871549333419 3139.236498918198006794026 31413.57034538691205229188 >>> besselyzero(5,100); besselyzero(5,1000); besselyzero(5,10000) 319.6183338562782156235062 3147.086508524556404473186 31421.42392920214673402828 >>> besselyzero(0,100,1); besselyzero(0,1000,1); besselyzero(0,10000,1) 313.3726705426359345050449 3140.807136030340213610065 31415.14112579761578220175
Zeros of functions with large order:
>>> besselyzero(50,1) 53.50285882040036394680237 >>> besselyzero(50,2) 60.11244442774058114686022 >>> besselyzero(50,100) 387.1096509824943957706835 >>> besselyzero(50,1,1) 56.96290427516751320063605 >>> besselyzero(50,2,1) 62.74888166945933944036623 >>> besselyzero(50,100,1) 388.6923300548309258355475
Zeros of functions with fractional order:
>>> besselyzero(0.5,1); besselyzero(1.5,1); besselyzero(2.25,4) 1.570796326794896619231322 2.798386045783887136720249 13.56721208770735123376018
Hankel functions¶
hankel1()¶
- mpmath.hankel1(n, x)¶
hankel1(n,x)computes the Hankel function of the first kind, which is the complex combination of Bessel functions given by\[H_n^{(1)}(x) = J_n(x) + i Y_n(x).\]Plots
# Hankel function H1_n(x) on the real line for n=0,1,2,3 h0 = lambda x: hankel1(0,x) h1 = lambda x: hankel1(1,x) h2 = lambda x: hankel1(2,x) h3 = lambda x: hankel1(3,x) plot([h0,h1,h2,h3],[0,6],[-2,1])
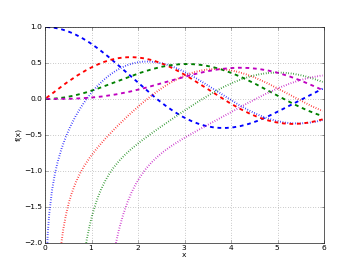
# Hankel function H1_n(z) in the complex plane cplot(lambda z: hankel1(1,z), [-8,8], [-8,8], points=50000)
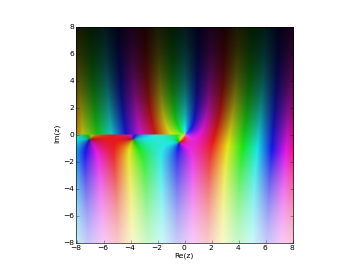
Examples
The Hankel function is generally complex-valued:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> hankel1(2, pi) (0.4854339326315091097054957 - 0.0999007139290278787734903j) >>> hankel1(3.5, pi) (0.2340002029630507922628888 - 0.6419643823412927142424049j)
hankel2()¶
- mpmath.hankel2(n, x)¶
hankel2(n,x)computes the Hankel function of the second kind, which is the complex combination of Bessel functions given by\[H_n^{(2)}(x) = J_n(x) - i Y_n(x).\]Plots
# Hankel function H2_n(x) on the real line for n=0,1,2,3 h0 = lambda x: hankel2(0,x) h1 = lambda x: hankel2(1,x) h2 = lambda x: hankel2(2,x) h3 = lambda x: hankel2(3,x) plot([h0,h1,h2,h3],[0,6],[-1,2])
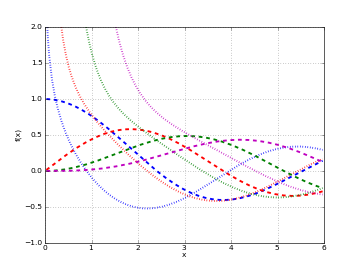
# Hankel function H2_n(z) in the complex plane cplot(lambda z: hankel2(1,z), [-8,8], [-8,8], points=50000)
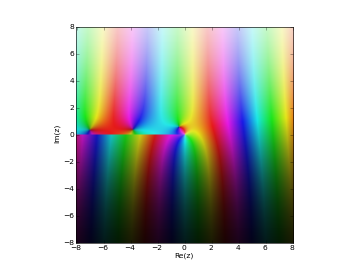
Examples
The Hankel function is generally complex-valued:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> hankel2(2, pi) (0.4854339326315091097054957 + 0.0999007139290278787734903j) >>> hankel2(3.5, pi) (0.2340002029630507922628888 + 0.6419643823412927142424049j)
Kelvin functions¶
ber()¶
- mpmath.ber(n, z, **kwargs)¶
Computes the Kelvin function ber, which for real arguments gives the real part of the Bessel J function of a rotated argument
\[J_n\left(x e^{3\pi i/4}\right) = \mathrm{ber}_n(x) + i \mathrm{bei}_n(x).\]The imaginary part is given by
bei().Plots
# Kelvin functions ber_n(x) and bei_n(x) on the real line for n=0,2 f0 = lambda x: ber(0,x) f1 = lambda x: bei(0,x) f2 = lambda x: ber(2,x) f3 = lambda x: bei(2,x) plot([f0,f1,f2,f3],[0,10],[-10,10])
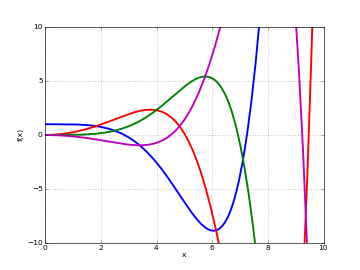
Examples
Verifying the defining relation:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> n, x = 2, 3.5 >>> ber(n,x) 1.442338852571888752631129 >>> bei(n,x) -0.948359035324558320217678 >>> besselj(n, x*root(1,8,3)) (1.442338852571888752631129 - 0.948359035324558320217678j)
The ber and bei functions are also defined by analytic continuation for complex arguments:
>>> ber(1+j, 2+3j) (4.675445984756614424069563 - 15.84901771719130765656316j) >>> bei(1+j, 2+3j) (15.83886679193707699364398 + 4.684053288183046528703611j)
bei()¶
ker()¶
- mpmath.ker(n, z, **kwargs)¶
Computes the Kelvin function ker, which for real arguments gives the real part of the (rescaled) Bessel K function of a rotated argument
\[e^{-\pi i/2} K_n\left(x e^{3\pi i/4}\right) = \mathrm{ker}_n(x) + i \mathrm{kei}_n(x).\]The imaginary part is given by
kei().Plots
# Kelvin functions ker_n(x) and kei_n(x) on the real line for n=0,2 f0 = lambda x: ker(0,x) f1 = lambda x: kei(0,x) f2 = lambda x: ker(2,x) f3 = lambda x: kei(2,x) plot([f0,f1,f2,f3],[0,5],[-1,4])
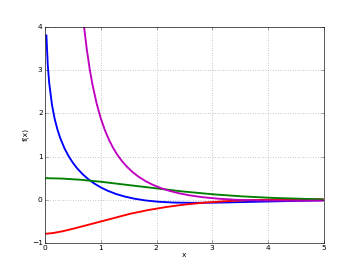
Examples
Verifying the defining relation:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> n, x = 2, 4.5 >>> ker(n,x) 0.02542895201906369640249801 >>> kei(n,x) -0.02074960467222823237055351 >>> exp(-n*pi*j/2) * besselk(n, x*root(1,8,1)) (0.02542895201906369640249801 - 0.02074960467222823237055351j)
The ker and kei functions are also defined by analytic continuation for complex arguments:
>>> ker(1+j, 3+4j) (1.586084268115490421090533 - 2.939717517906339193598719j) >>> kei(1+j, 3+4j) (-2.940403256319453402690132 - 1.585621643835618941044855j)
kei()¶
Struve functions¶
struveh()¶
- mpmath.struveh(n, z, **kwargs)¶
Gives the Struve function
\[\,\mathbf{H}_n(z) = \sum_{k=0}^\infty \frac{(-1)^k}{\Gamma(k+\frac{3}{2}) \Gamma(k+n+\frac{3}{2})} {\left({\frac{z}{2}}\right)}^{2k+n+1}\]which is a solution to the Struve differential equation
\[z^2 f''(z) + z f'(z) + (z^2-n^2) f(z) = \frac{2 z^{n+1}}{\pi (2n-1)!!}.\]Examples
Evaluation for arbitrary real and complex arguments:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> struveh(0, 3.5) 0.3608207733778295024977797 >>> struveh(-1, 10) -0.255212719726956768034732 >>> struveh(1, -100.5) 0.5819566816797362287502246 >>> struveh(2.5, 10000000000000) 3153915652525200060.308937 >>> struveh(2.5, -10000000000000) (0.0 - 3153915652525200060.308937j) >>> struveh(1+j, 1000000+4000000j) (-3.066421087689197632388731e+1737173 - 1.596619701076529803290973e+1737173j)
A Struve function of half-integer order is elementary; for example:
>>> z = 3 >>> struveh(0.5, 3) 0.9167076867564138178671595 >>> sqrt(2/(pi*z))*(1-cos(z)) 0.9167076867564138178671595
Numerically verifying the differential equation:
>>> z = mpf(4.5) >>> n = 3 >>> f = lambda z: struveh(n,z) >>> lhs = z**2*diff(f,z,2) + z*diff(f,z) + (z**2-n**2)*f(z) >>> rhs = 2*z**(n+1)/fac2(2*n-1)/pi >>> lhs 17.40359302709875496632744 >>> rhs 17.40359302709875496632744
struvel()¶
- mpmath.struvel(n, z, **kwargs)¶
Gives the modified Struve function
\[\,\mathbf{L}_n(z) = -i e^{-n\pi i/2} \mathbf{H}_n(i z)\]which solves to the modified Struve differential equation
\[z^2 f''(z) + z f'(z) - (z^2+n^2) f(z) = \frac{2 z^{n+1}}{\pi (2n-1)!!}.\]Examples
Evaluation for arbitrary real and complex arguments:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> struvel(0, 3.5) 7.180846515103737996249972 >>> struvel(-1, 10) 2670.994904980850550721511 >>> struvel(1, -100.5) 1.757089288053346261497686e+42 >>> struvel(2.5, 10000000000000) 4.160893281017115450519948e+4342944819025 >>> struvel(2.5, -10000000000000) (0.0 - 4.160893281017115450519948e+4342944819025j) >>> struvel(1+j, 700j) (-0.1721150049480079451246076 + 0.1240770953126831093464055j) >>> struvel(1+j, 1000000+4000000j) (-2.973341637511505389128708e+434290 - 5.164633059729968297147448e+434290j)
Numerically verifying the differential equation:
>>> z = mpf(3.5) >>> n = 3 >>> f = lambda z: struvel(n,z) >>> lhs = z**2*diff(f,z,2) + z*diff(f,z) - (z**2+n**2)*f(z) >>> rhs = 2*z**(n+1)/fac2(2*n-1)/pi >>> lhs 6.368850306060678353018165 >>> rhs 6.368850306060678353018165
Anger-Weber functions¶
angerj()¶
- mpmath.angerj(v, z, **kwargs)¶
Gives the Anger function
\[\mathbf{J}_{\nu}(z) = \frac{1}{\pi} \int_0^{\pi} \cos(\nu t - z \sin t) dt\]which is an entire function of both the parameter \(\nu\) and the argument \(z\). It solves the inhomogeneous Bessel differential equation
\[f''(z) + \frac{1}{z}f'(z) + \left(1-\frac{\nu^2}{z^2}\right) f(z) = \frac{(z-\nu)}{\pi z^2} \sin(\pi \nu).\]Examples
Evaluation for real and complex parameter and argument:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> angerj(2,3) 0.4860912605858910769078311 >>> angerj(-3+4j, 2+5j) (-5033.358320403384472395612 + 585.8011892476145118551756j) >>> angerj(3.25, 1e6j) (4.630743639715893346570743e+434290 - 1.117960409887505906848456e+434291j) >>> angerj(-1.5, 1e6) 0.0002795719747073879393087011
The Anger function coincides with the Bessel J-function when \(\nu\) is an integer:
>>> angerj(1,3); besselj(1,3) 0.3390589585259364589255146 0.3390589585259364589255146 >>> angerj(1.5,3); besselj(1.5,3) 0.4088969848691080859328847 0.4777182150870917715515015
Verifying the differential equation:
>>> v,z = mpf(2.25), 0.75 >>> f = lambda z: angerj(v,z) >>> diff(f,z,2) + diff(f,z)/z + (1-(v/z)**2)*f(z) -0.6002108774380707130367995 >>> (z-v)/(pi*z**2) * sinpi(v) -0.6002108774380707130367995
Verifying the integral representation:
>>> angerj(v,z) 0.1145380759919333180900501 >>> quad(lambda t: cos(v*t-z*sin(t))/pi, [0,pi]) 0.1145380759919333180900501
References
[DLMF] section 11.10: Anger-Weber Functions
webere()¶
- mpmath.webere(v, z, **kwargs)¶
Gives the Weber function
\[\mathbf{E}_{\nu}(z) = \frac{1}{\pi} \int_0^{\pi} \sin(\nu t - z \sin t) dt\]which is an entire function of both the parameter \(\nu\) and the argument \(z\). It solves the inhomogeneous Bessel differential equation
\[f''(z) + \frac{1}{z}f'(z) + \left(1-\frac{\nu^2}{z^2}\right) f(z) = -\frac{1}{\pi z^2} (z+\nu+(z-\nu)\cos(\pi \nu)).\]Examples
Evaluation for real and complex parameter and argument:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> webere(2,3) -0.1057668973099018425662646 >>> webere(-3+4j, 2+5j) (-585.8081418209852019290498 - 5033.314488899926921597203j) >>> webere(3.25, 1e6j) (-1.117960409887505906848456e+434291 - 4.630743639715893346570743e+434290j) >>> webere(3.25, 1e6) -0.00002812518265894315604914453
Up to addition of a rational function of \(z\), the Weber function coincides with the Struve H-function when \(\nu\) is an integer:
>>> webere(1,3); 2/pi-struveh(1,3) -0.3834897968188690177372881 -0.3834897968188690177372881 >>> webere(5,3); 26/(35*pi)-struveh(5,3) 0.2009680659308154011878075 0.2009680659308154011878075
Verifying the differential equation:
>>> v,z = mpf(2.25), 0.75 >>> f = lambda z: webere(v,z) >>> diff(f,z,2) + diff(f,z)/z + (1-(v/z)**2)*f(z) -1.097441848875479535164627 >>> -(z+v+(z-v)*cospi(v))/(pi*z**2) -1.097441848875479535164627
Verifying the integral representation:
>>> webere(v,z) 0.1486507351534283744485421 >>> quad(lambda t: sin(v*t-z*sin(t))/pi, [0,pi]) 0.1486507351534283744485421
References
[DLMF] section 11.10: Anger-Weber Functions
Lommel functions¶
lommels1()¶
- mpmath.lommels1(u, v, z, **kwargs)¶
Gives the Lommel function \(s_{\mu,\nu}\) or \(s^{(1)}_{\mu,\nu}\)
\[s_{\mu,\nu}(z) = \frac{z^{\mu+1}}{(\mu-\nu+1)(\mu+\nu+1)} \,_1F_2\left(1; \frac{\mu-\nu+3}{2}, \frac{\mu+\nu+3}{2}; -\frac{z^2}{4} \right)\]which solves the inhomogeneous Bessel equation
\[z^2 f''(z) + z f'(z) + (z^2-\nu^2) f(z) = z^{\mu+1}.\]A second solution is given by
lommels2().Plots
# Lommel function s_(u,v)(x) on the real line for a few different u,v f1 = lambda x: lommels1(-1,2.5,x) f2 = lambda x: lommels1(0,0.5,x) f3 = lambda x: lommels1(0,6,x) f4 = lambda x: lommels1(0.5,3,x) plot([f1,f2,f3,f4], [0,20])
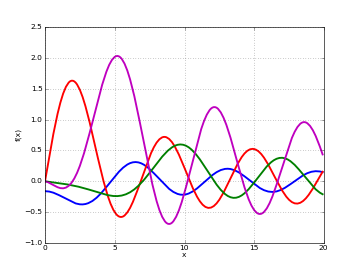
Examples
An integral representation:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> u,v,z = 0.25, 0.125, mpf(0.75) >>> lommels1(u,v,z) 0.4276243877565150372999126 >>> (bessely(v,z)*quad(lambda t: t**u*besselj(v,t), [0,z]) - \ ... besselj(v,z)*quad(lambda t: t**u*bessely(v,t), [0,z]))*(pi/2) 0.4276243877565150372999126
A special value:
>>> lommels1(v,v,z) 0.5461221367746048054932553 >>> gamma(v+0.5)*sqrt(pi)*power(2,v-1)*struveh(v,z) 0.5461221367746048054932553
Verifying the differential equation:
>>> f = lambda z: lommels1(u,v,z) >>> z**2*diff(f,z,2) + z*diff(f,z) + (z**2-v**2)*f(z) 0.6979536443265746992059141 >>> z**(u+1) 0.6979536443265746992059141
References
lommels2()¶
- mpmath.lommels2(u, v, z, **kwargs)¶
Gives the second Lommel function \(S_{\mu,\nu}\) or \(s^{(2)}_{\mu,\nu}\)
\[ \begin{align}\begin{aligned}S_{\mu,\nu}(z) = s_{\mu,\nu}(z) + 2^{\mu-1} \Gamma\left(\tfrac{1}{2}(\mu-\nu+1)\right) \Gamma\left(\tfrac{1}{2}(\mu+\nu+1)\right) \times\\ \left[\sin(\tfrac{1}{2}(\mu-\nu)\pi) J_{\nu}(z) - \cos(\tfrac{1}{2}(\mu-\nu)\pi) Y_{\nu}(z) \right]\end{aligned}\end{align} \]which solves the same differential equation as
lommels1().Plots
# Lommel function S_(u,v)(x) on the real line for a few different u,v f1 = lambda x: lommels2(-1,2.5,x) f2 = lambda x: lommels2(1.5,2,x) f3 = lambda x: lommels2(2.5,1,x) f4 = lambda x: lommels2(3.5,-0.5,x) plot([f1,f2,f3,f4], [0,8], [-8,8])
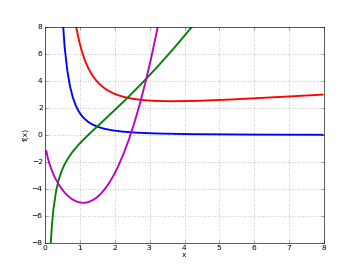
Examples
For large \(|z|\), \(S_{\mu,\nu} \sim z^{\mu-1}\):
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> lommels2(10,2,30000) 1.968299831601008419949804e+40 >>> power(30000,9) 1.9683e+40
A special value:
>>> u,v,z = 0.5, 0.125, mpf(0.75) >>> lommels2(v,v,z) 0.9589683199624672099969765 >>> (struveh(v,z)-bessely(v,z))*power(2,v-1)*sqrt(pi)*gamma(v+0.5) 0.9589683199624672099969765
Verifying the differential equation:
>>> f = lambda z: lommels2(u,v,z) >>> z**2*diff(f,z,2) + z*diff(f,z) + (z**2-v**2)*f(z) 0.6495190528383289850727924 >>> z**(u+1) 0.6495190528383289850727924
References
Airy and Scorer functions¶
airyai()¶
- mpmath.airyai(z, derivative=0, **kwargs)¶
Computes the Airy function \(\operatorname{Ai}(z)\), which is the solution of the Airy differential equation \(f''(z) - z f(z) = 0\) with initial conditions
\[ \begin{align}\begin{aligned}\operatorname{Ai}(0) = \frac{1}{3^{2/3}\Gamma\left(\frac{2}{3}\right)}\\\operatorname{Ai}'(0) = -\frac{1}{3^{1/3}\Gamma\left(\frac{1}{3}\right)}.\end{aligned}\end{align} \]Other common ways of defining the Ai-function include integrals such as
\[ \begin{align}\begin{aligned}\operatorname{Ai}(x) = \frac{1}{\pi} \int_0^{\infty} \cos\left(\frac{1}{3}t^3+xt\right) dt \qquad x \in \mathbb{R}\\\operatorname{Ai}(z) = \frac{\sqrt{3}}{2\pi} \int_0^{\infty} \exp\left(-\frac{t^3}{3}-\frac{z^3}{3t^3}\right) dt.\end{aligned}\end{align} \]The Ai-function is an entire function with a turning point, behaving roughly like a slowly decaying sine wave for \(z < 0\) and like a rapidly decreasing exponential for \(z > 0\). A second solution of the Airy differential equation is given by \(\operatorname{Bi}(z)\) (see
airybi()).Optionally, with derivative=alpha,
airyai()can compute the \(\alpha\)-th order fractional derivative with respect to \(z\). For \(\alpha = n = 1,2,3,\ldots\) this gives the derivative \(\operatorname{Ai}^{(n)}(z)\), and for \(\alpha = -n = -1,-2,-3,\ldots\) this gives the \(n\)-fold iterated integral\[ \begin{align}\begin{aligned}f_0(z) = \operatorname{Ai}(z)\\f_n(z) = \int_0^z f_{n-1}(t) dt.\end{aligned}\end{align} \]The Ai-function has infinitely many zeros, all located along the negative half of the real axis. They can be computed with
airyaizero().Plots
# Airy function Ai(x), Ai'(x) and int_0^x Ai(t) dt on the real line f = airyai f_diff = lambda z: airyai(z, derivative=1) f_int = lambda z: airyai(z, derivative=-1) plot([f, f_diff, f_int], [-10,5])
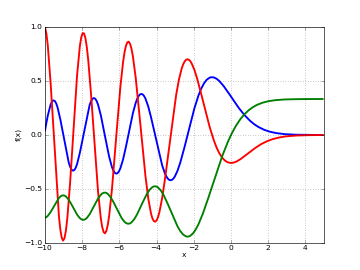
# Airy function Ai(z) in the complex plane cplot(airyai, [-8,8], [-8,8], points=50000)
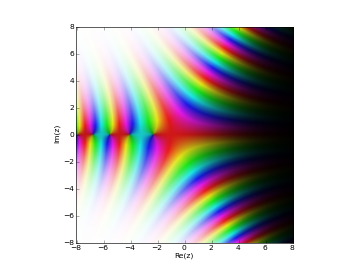
Basic examples
Limits and values include:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> airyai(0); 1/(power(3,'2/3')*gamma('2/3')) 0.3550280538878172392600632 0.3550280538878172392600632 >>> airyai(1) 0.1352924163128814155241474 >>> airyai(-1) 0.5355608832923521187995166 >>> airyai(inf); airyai(-inf) 0.0 0.0
Evaluation is supported for large magnitudes of the argument:
>>> airyai(-100) 0.1767533932395528780908311 >>> airyai(100) 2.634482152088184489550553e-291 >>> airyai(50+50j) (-5.31790195707456404099817e-68 - 1.163588003770709748720107e-67j) >>> airyai(-50+50j) (1.041242537363167632587245e+158 + 3.347525544923600321838281e+157j)
Huge arguments are also fine:
>>> airyai(10**10) 1.162235978298741779953693e-289529654602171 >>> airyai(-10**10) 0.0001736206448152818510510181 >>> w = airyai(10**10*(1+j)) >>> w.real 5.711508683721355528322567e-186339621747698 >>> w.imag 1.867245506962312577848166e-186339621747697
The first root of the Ai-function is:
>>> findroot(airyai, -2) -2.338107410459767038489197 >>> airyaizero(1) -2.338107410459767038489197
Properties and relations
Verifying the Airy differential equation:
>>> for z in [-3.4, 0, 2.5, 1+2j]: ... chop(airyai(z,2) - z*airyai(z)) ... 0.0 0.0 0.0 0.0
The first few terms of the Taylor series expansion around \(z = 0\) (every third term is zero):
>>> nprint(taylor(airyai, 0, 5)) [0.355028, -0.258819, 0.0, 0.0591713, -0.0215683, 0.0]
The Airy functions satisfy the Wronskian relation \(\operatorname{Ai}(z) \operatorname{Bi}'(z) - \operatorname{Ai}'(z) \operatorname{Bi}(z) = 1/\pi\):
>>> z = -0.5 >>> airyai(z)*airybi(z,1) - airyai(z,1)*airybi(z) 0.3183098861837906715377675 >>> 1/pi 0.3183098861837906715377675
The Airy functions can be expressed in terms of Bessel functions of order \(\pm 1/3\). For \(\Re[z] \le 0\), we have:
>>> z = -3 >>> airyai(z) -0.3788142936776580743472439 >>> y = 2*power(-z,'3/2')/3 >>> (sqrt(-z) * (besselj('1/3',y) + besselj('-1/3',y)))/3 -0.3788142936776580743472439
Derivatives and integrals
Derivatives of the Ai-function (directly and using
diff()):>>> airyai(-3,1); diff(airyai,-3) 0.3145837692165988136507873 0.3145837692165988136507873 >>> airyai(-3,2); diff(airyai,-3,2) 1.136442881032974223041732 1.136442881032974223041732 >>> airyai(1000,1); diff(airyai,1000) -2.943133917910336090459748e-9156 -2.943133917910336090459748e-9156
Several derivatives at \(z = 0\):
>>> airyai(0,0); airyai(0,1); airyai(0,2) 0.3550280538878172392600632 -0.2588194037928067984051836 0.0 >>> airyai(0,3); airyai(0,4); airyai(0,5) 0.3550280538878172392600632 -0.5176388075856135968103671 0.0 >>> airyai(0,15); airyai(0,16); airyai(0,17) 1292.30211615165475090663 -3188.655054727379756351861 0.0
The integral of the Ai-function:
>>> airyai(3,-1); quad(airyai, [0,3]) 0.3299203760070217725002701 0.3299203760070217725002701 >>> airyai(-10,-1); quad(airyai, [0,-10]) -0.765698403134212917425148 -0.765698403134212917425148
Integrals of high or fractional order:
>>> airyai(-2,0.5); differint(airyai,-2,0.5,0) (0.0 + 0.2453596101351438273844725j) (0.0 + 0.2453596101351438273844725j) >>> airyai(-2,-4); differint(airyai,-2,-4,0) 0.2939176441636809580339365 0.2939176441636809580339365 >>> airyai(0,-1); airyai(0,-2); airyai(0,-3) 0.0 0.0 0.0
Integrals of the Ai-function can be evaluated at limit points:
>>> airyai(-1000000,-1); airyai(-inf,-1) -0.6666843728311539978751512 -0.6666666666666666666666667 >>> airyai(10,-1); airyai(+inf,-1) 0.3333333332991690159427932 0.3333333333333333333333333 >>> airyai(+inf,-2); airyai(+inf,-3) +inf +inf >>> airyai(-1000000,-2); airyai(-inf,-2) 666666.4078472650651209742 +inf >>> airyai(-1000000,-3); airyai(-inf,-3) -333333074513.7520264995733 -inf
References
[DLMF] Chapter 9: Airy and Related Functions
[WolframFunctions] section: Bessel-Type Functions
airybi()¶
- mpmath.airybi(z, derivative=0, **kwargs)¶
Computes the Airy function \(\operatorname{Bi}(z)\), which is the solution of the Airy differential equation \(f''(z) - z f(z) = 0\) with initial conditions
\[ \begin{align}\begin{aligned}\operatorname{Bi}(0) = \frac{1}{3^{1/6}\Gamma\left(\frac{2}{3}\right)}\\\operatorname{Bi}'(0) = \frac{3^{1/6}}{\Gamma\left(\frac{1}{3}\right)}.\end{aligned}\end{align} \]Like the Ai-function (see
airyai()), the Bi-function is oscillatory for \(z < 0\), but it grows rather than decreases for \(z > 0\).Optionally, as for
airyai(), derivatives, integrals and fractional derivatives can be computed with the derivative parameter.The Bi-function has infinitely many zeros along the negative half-axis, as well as complex zeros, which can all be computed with
airybizero().Plots
# Airy function Bi(x), Bi'(x) and int_0^x Bi(t) dt on the real line f = airybi f_diff = lambda z: airybi(z, derivative=1) f_int = lambda z: airybi(z, derivative=-1) plot([f, f_diff, f_int], [-10,2], [-1,2])
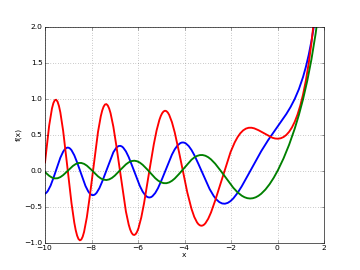
# Airy function Bi(z) in the complex plane cplot(airybi, [-8,8], [-8,8], points=50000)
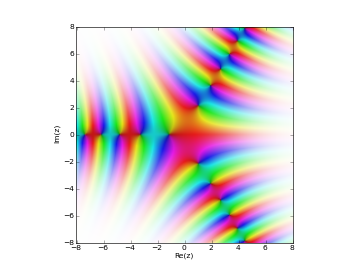
Basic examples
Limits and values include:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> airybi(0); 1/(power(3,'1/6')*gamma('2/3')) 0.6149266274460007351509224 0.6149266274460007351509224 >>> airybi(1) 1.207423594952871259436379 >>> airybi(-1) 0.10399738949694461188869 >>> airybi(inf); airybi(-inf) +inf 0.0
Evaluation is supported for large magnitudes of the argument:
>>> airybi(-100) 0.02427388768016013160566747 >>> airybi(100) 6.041223996670201399005265e+288 >>> airybi(50+50j) (-5.322076267321435669290334e+63 + 1.478450291165243789749427e+65j) >>> airybi(-50+50j) (-3.347525544923600321838281e+157 + 1.041242537363167632587245e+158j)
Huge arguments:
>>> airybi(10**10) 1.369385787943539818688433e+289529654602165 >>> airybi(-10**10) 0.001775656141692932747610973 >>> w = airybi(10**10*(1+j)) >>> w.real -6.559955931096196875845858e+186339621747689 >>> w.imag -6.822462726981357180929024e+186339621747690
The first real root of the Bi-function is:
>>> findroot(airybi, -1); airybizero(1) -1.17371322270912792491998 -1.17371322270912792491998
Properties and relations
Verifying the Airy differential equation:
>>> for z in [-3.4, 0, 2.5, 1+2j]: ... chop(airybi(z,2) - z*airybi(z)) ... 0.0 0.0 0.0 0.0
The first few terms of the Taylor series expansion around \(z = 0\) (every third term is zero):
>>> nprint(taylor(airybi, 0, 5)) [0.614927, 0.448288, 0.0, 0.102488, 0.0373574, 0.0]
The Airy functions can be expressed in terms of Bessel functions of order \(\pm 1/3\). For \(\Re[z] \le 0\), we have:
>>> z = -3 >>> airybi(z) -0.1982896263749265432206449 >>> p = 2*power(-z,'3/2')/3 >>> sqrt(-mpf(z)/3)*(besselj('-1/3',p) - besselj('1/3',p)) -0.1982896263749265432206449
Derivatives and integrals
Derivatives of the Bi-function (directly and using
diff()):>>> airybi(-3,1); diff(airybi,-3) -0.675611222685258537668032 -0.675611222685258537668032 >>> airybi(-3,2); diff(airybi,-3,2) 0.5948688791247796296619346 0.5948688791247796296619346 >>> airybi(1000,1); diff(airybi,1000) 1.710055114624614989262335e+9156 1.710055114624614989262335e+9156
Several derivatives at \(z = 0\):
>>> airybi(0,0); airybi(0,1); airybi(0,2) 0.6149266274460007351509224 0.4482883573538263579148237 0.0 >>> airybi(0,3); airybi(0,4); airybi(0,5) 0.6149266274460007351509224 0.8965767147076527158296474 0.0 >>> airybi(0,15); airybi(0,16); airybi(0,17) 2238.332923903442675949357 5522.912562599140729510628 0.0
The integral of the Bi-function:
>>> airybi(3,-1); quad(airybi, [0,3]) 10.06200303130620056316655 10.06200303130620056316655 >>> airybi(-10,-1); quad(airybi, [0,-10]) -0.01504042480614002045135483 -0.01504042480614002045135483
Integrals of high or fractional order:
>>> airybi(-2,0.5); differint(airybi, -2, 0.5, 0) (0.0 + 0.5019859055341699223453257j) (0.0 + 0.5019859055341699223453257j) >>> airybi(-2,-4); differint(airybi,-2,-4,0) 0.2809314599922447252139092 0.2809314599922447252139092 >>> airybi(0,-1); airybi(0,-2); airybi(0,-3) 0.0 0.0 0.0
Integrals of the Bi-function can be evaluated at limit points:
>>> airybi(-1000000,-1); airybi(-inf,-1) 0.000002191261128063434047966873 0.0 >>> airybi(10,-1); airybi(+inf,-1) 147809803.1074067161675853 +inf >>> airybi(+inf,-2); airybi(+inf,-3) +inf +inf >>> airybi(-1000000,-2); airybi(-inf,-2) 0.4482883750599908479851085 0.4482883573538263579148237 >>> gamma('2/3')*power(3,'2/3')/(2*pi) 0.4482883573538263579148237 >>> airybi(-100000,-3); airybi(-inf,-3) -44828.52827206932872493133 -inf >>> airybi(-100000,-4); airybi(-inf,-4) 2241411040.437759489540248 +inf
airyaizero()¶
- mpmath.airyaizero(k, derivative=0)¶
Gives the \(k\)-th zero of the Airy Ai-function, i.e. the \(k\)-th number \(a_k\) ordered by magnitude for which \(\operatorname{Ai}(a_k) = 0\).
Optionally, with derivative=1, the corresponding zero \(a'_k\) of the derivative function, i.e. \(\operatorname{Ai}'(a'_k) = 0\), is computed.
Examples
Some values of \(a_k\):
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> airyaizero(1) -2.338107410459767038489197 >>> airyaizero(2) -4.087949444130970616636989 >>> airyaizero(3) -5.520559828095551059129856 >>> airyaizero(1000) -281.0315196125215528353364
Some values of \(a'_k\):
>>> airyaizero(1,1) -1.018792971647471089017325 >>> airyaizero(2,1) -3.248197582179836537875424 >>> airyaizero(3,1) -4.820099211178735639400616 >>> airyaizero(1000,1) -280.9378080358935070607097
Verification:
>>> chop(airyai(airyaizero(1))) 0.0 >>> chop(airyai(airyaizero(1,1),1)) 0.0
airybizero()¶
- mpmath.airybizero(k, derivative=0, complex=0)¶
With complex=False, gives the \(k\)-th real zero of the Airy Bi-function, i.e. the \(k\)-th number \(b_k\) ordered by magnitude for which \(\operatorname{Bi}(b_k) = 0\).
With complex=True, gives the \(k\)-th complex zero in the upper half plane \(\beta_k\). Also the conjugate \(\overline{\beta_k}\) is a zero.
Optionally, with derivative=1, the corresponding zero \(b'_k\) or \(\beta'_k\) of the derivative function, i.e. \(\operatorname{Bi}'(b'_k) = 0\) or \(\operatorname{Bi}'(\beta'_k) = 0\), is computed.
Examples
Some values of \(b_k\):
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> airybizero(1) -1.17371322270912792491998 >>> airybizero(2) -3.271093302836352715680228 >>> airybizero(3) -4.830737841662015932667709 >>> airybizero(1000) -280.9378112034152401578834
Some values of \(b_k\):
>>> airybizero(1,1) -2.294439682614123246622459 >>> airybizero(2,1) -4.073155089071828215552369 >>> airybizero(3,1) -5.512395729663599496259593 >>> airybizero(1000,1) -281.0315164471118527161362
Some values of \(\beta_k\):
>>> airybizero(1,complex=True) (0.9775448867316206859469927 + 2.141290706038744575749139j) >>> airybizero(2,complex=True) (1.896775013895336346627217 + 3.627291764358919410440499j) >>> airybizero(3,complex=True) (2.633157739354946595708019 + 4.855468179979844983174628j) >>> airybizero(1000,complex=True) (140.4978560578493018899793 + 243.3907724215792121244867j)
Some values of \(\beta'_k\):
>>> airybizero(1,1,complex=True) (0.2149470745374305676088329 + 1.100600143302797880647194j) >>> airybizero(2,1,complex=True) (1.458168309223507392028211 + 2.912249367458445419235083j) >>> airybizero(3,1,complex=True) (2.273760763013482299792362 + 4.254528549217097862167015j) >>> airybizero(1000,1,complex=True) (140.4509972835270559730423 + 243.3096175398562811896208j)
Verification:
>>> chop(airybi(airybizero(1))) 0.0 >>> chop(airybi(airybizero(1,1),1)) 0.0 >>> u = airybizero(1,complex=True) >>> chop(airybi(u)) 0.0 >>> chop(airybi(conj(u))) 0.0
The complex zeros (in the upper and lower half-planes respectively) asymptotically approach the rays \(z = R \exp(\pm i \pi /3)\):
>>> arg(airybizero(1,complex=True)) 1.142532510286334022305364 >>> arg(airybizero(1000,complex=True)) 1.047271114786212061583917 >>> arg(airybizero(1000000,complex=True)) 1.047197624741816183341355 >>> pi/3 1.047197551196597746154214
scorergi()¶
- mpmath.scorergi(z, **kwargs)¶
Evaluates the Scorer function
\[\operatorname{Gi}(z) = \operatorname{Ai}(z) \int_0^z \operatorname{Bi}(t) dt + \operatorname{Bi}(z) \int_z^{\infty} \operatorname{Ai}(t) dt\]which gives a particular solution to the inhomogeneous Airy differential equation \(f''(z) - z f(z) = 1/\pi\). Another particular solution is given by the Scorer Hi-function (
scorerhi()). The two functions are related as \(\operatorname{Gi}(z) + \operatorname{Hi}(z) = \operatorname{Bi}(z)\).Plots
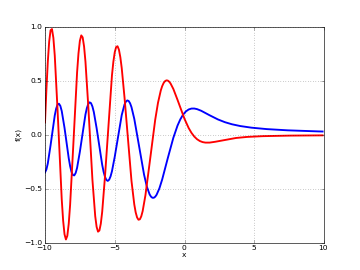
# Scorer function Gi(x) and Gi'(x) on the real line plot([scorergi, diffun(scorergi)], [-10,10])
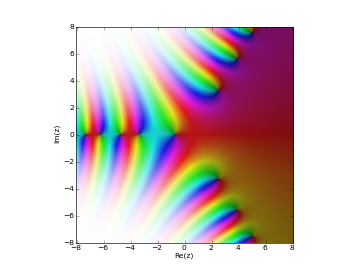
# Scorer function Gi(z) in the complex plane cplot(scorergi, [-8,8], [-8,8], points=50000)
Examples
Some values and limits:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> scorergi(0); 1/(power(3,'7/6')*gamma('2/3')) 0.2049755424820002450503075 0.2049755424820002450503075 >>> diff(scorergi, 0); 1/(power(3,'5/6')*gamma('1/3')) 0.1494294524512754526382746 0.1494294524512754526382746 >>> scorergi(+inf); scorergi(-inf) 0.0 0.0 >>> scorergi(1) 0.2352184398104379375986902 >>> scorergi(-1) -0.1166722172960152826494198
Evaluation for large arguments:
>>> scorergi(10) 0.03189600510067958798062034 >>> scorergi(100) 0.003183105228162961476590531 >>> scorergi(1000000) 0.0000003183098861837906721743873 >>> 1/(pi*1000000) 0.0000003183098861837906715377675 >>> scorergi(-1000) -0.08358288400262780392338014 >>> scorergi(-100000) 0.02886866118619660226809581 >>> scorergi(50+10j) (0.0061214102799778578790984 - 0.001224335676457532180747917j) >>> scorergi(-50-10j) (5.236047850352252236372551e+29 - 3.08254224233701381482228e+29j) >>> scorergi(100000j) (-8.806659285336231052679025e+6474077 + 8.684731303500835514850962e+6474077j)
Verifying the connection between Gi and Hi:
>>> z = 0.25 >>> scorergi(z) + scorerhi(z) 0.7287469039362150078694543 >>> airybi(z) 0.7287469039362150078694543
Verifying the differential equation:
>>> for z in [-3.4, 0, 2.5, 1+2j]: ... chop(diff(scorergi,z,2) - z*scorergi(z)) ... -0.3183098861837906715377675 -0.3183098861837906715377675 -0.3183098861837906715377675 -0.3183098861837906715377675
Verifying the integral representation:
>>> z = 0.5 >>> scorergi(z) 0.2447210432765581976910539 >>> Ai,Bi = airyai,airybi >>> Bi(z)*(Ai(inf,-1)-Ai(z,-1)) + Ai(z)*(Bi(z,-1)-Bi(0,-1)) 0.2447210432765581976910539
References
[DLMF] section 9.12: Scorer Functions
scorerhi()¶
- mpmath.scorerhi(z, **kwargs)¶
Evaluates the second Scorer function
\[\operatorname{Hi}(z) = \operatorname{Bi}(z) \int_{-\infty}^z \operatorname{Ai}(t) dt - \operatorname{Ai}(z) \int_{-\infty}^z \operatorname{Bi}(t) dt\]which gives a particular solution to the inhomogeneous Airy differential equation \(f''(z) - z f(z) = 1/\pi\). See also
scorergi().Plots
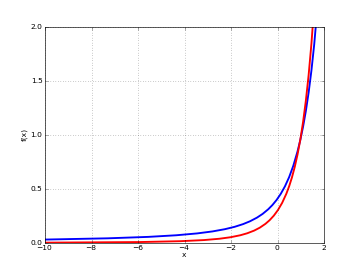
# Scorer function Hi(x) and Hi'(x) on the real line plot([scorerhi, diffun(scorerhi)], [-10,2], [0,2])
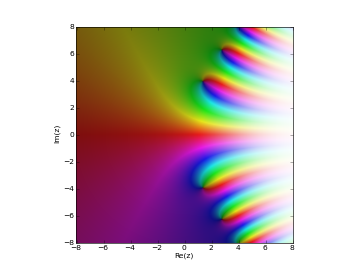
# Scorer function Hi(z) in the complex plane cplot(scorerhi, [-8,8], [-8,8], points=50000)
Examples
Some values and limits:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> scorerhi(0); 2/(power(3,'7/6')*gamma('2/3')) 0.4099510849640004901006149 0.4099510849640004901006149 >>> diff(scorerhi,0); 2/(power(3,'5/6')*gamma('1/3')) 0.2988589049025509052765491 0.2988589049025509052765491 >>> scorerhi(+inf); scorerhi(-inf) +inf 0.0 >>> scorerhi(1) 0.9722051551424333218376886 >>> scorerhi(-1) 0.2206696067929598945381098
Evaluation for large arguments:
>>> scorerhi(10) 455641153.5163291358991077 >>> scorerhi(100) 6.041223996670201399005265e+288 >>> scorerhi(1000000) 7.138269638197858094311122e+289529652 >>> scorerhi(-10) 0.0317685352825022727415011 >>> scorerhi(-100) 0.003183092495767499864680483 >>> scorerhi(100j) (-6.366197716545672122983857e-9 + 0.003183098861710582761688475j) >>> scorerhi(50+50j) (-5.322076267321435669290334e+63 + 1.478450291165243789749427e+65j) >>> scorerhi(-1000-1000j) (0.0001591549432510502796565538 - 0.000159154943091895334973109j)
Verifying the differential equation:
>>> for z in [-3.4, 0, 2, 1+2j]: ... chop(diff(scorerhi,z,2) - z*scorerhi(z)) ... 0.3183098861837906715377675 0.3183098861837906715377675 0.3183098861837906715377675 0.3183098861837906715377675
Verifying the integral representation:
>>> z = 0.5 >>> scorerhi(z) 0.6095559998265972956089949 >>> Ai,Bi = airyai,airybi >>> Bi(z)*(Ai(z,-1)-Ai(-inf,-1)) - Ai(z)*(Bi(z,-1)-Bi(-inf,-1)) 0.6095559998265972956089949
Coulomb wave functions¶
coulombf()¶
- mpmath.coulombf(l, eta, z)¶
Calculates the regular Coulomb wave function
\[F_l(\eta,z) = C_l(\eta) z^{l+1} e^{-iz} \,_1F_1(l+1-i\eta, 2l+2, 2iz)\]where the normalization constant \(C_l(\eta)\) is as calculated by
coulombc(). This function solves the differential equation\[f''(z) + \left(1-\frac{2\eta}{z}-\frac{l(l+1)}{z^2}\right) f(z) = 0.\]A second linearly independent solution is given by the irregular Coulomb wave function \(G_l(\eta,z)\) (see
coulombg()) and thus the general solution is \(f(z) = C_1 F_l(\eta,z) + C_2 G_l(\eta,z)\) for arbitrary constants \(C_1\), \(C_2\). Physically, the Coulomb wave functions give the radial solution to the Schrodinger equation for a point particle in a \(1/z\) potential; \(z\) is then the radius and \(l\), \(\eta\) are quantum numbers.The Coulomb wave functions with real parameters are defined in Abramowitz & Stegun, section 14. However, all parameters are permitted to be complex in this implementation (see references).
Plots
# Regular Coulomb wave functions -- equivalent to figure 14.3 in A&S F1 = lambda x: coulombf(0,0,x) F2 = lambda x: coulombf(0,1,x) F3 = lambda x: coulombf(0,5,x) F4 = lambda x: coulombf(0,10,x) F5 = lambda x: coulombf(0,x/2,x) plot([F1,F2,F3,F4,F5], [0,25], [-1.2,1.6])
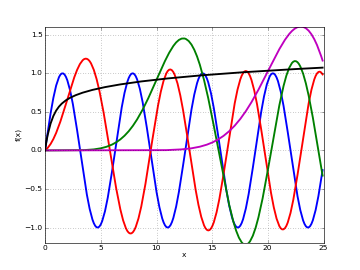
# Regular Coulomb wave function in the complex plane cplot(lambda z: coulombf(1,1,z), points=50000)
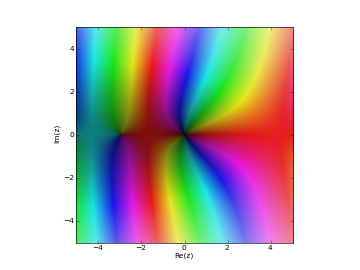
Examples
Evaluation is supported for arbitrary magnitudes of \(z\):
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> coulombf(2, 1.5, 3.5) 0.4080998961088761187426445 >>> coulombf(-2, 1.5, 3.5) 0.7103040849492536747533465 >>> coulombf(2, 1.5, '1e-10') 4.143324917492256448770769e-33 >>> coulombf(2, 1.5, 1000) 0.4482623140325567050716179 >>> coulombf(2, 1.5, 10**10) -0.066804196437694360046619
Verifying the differential equation:
>>> l, eta, z = 2, 3, mpf(2.75) >>> A, B = 1, 2 >>> f = lambda z: A*coulombf(l,eta,z) + B*coulombg(l,eta,z) >>> chop(diff(f,z,2) + (1-2*eta/z - l*(l+1)/z**2)*f(z)) 0.0
A Wronskian relation satisfied by the Coulomb wave functions:
>>> l = 2 >>> eta = 1.5 >>> F = lambda z: coulombf(l,eta,z) >>> G = lambda z: coulombg(l,eta,z) >>> for z in [3.5, -1, 2+3j]: ... chop(diff(F,z)*G(z) - F(z)*diff(G,z)) ... 1.0 1.0 1.0
Another Wronskian relation:
>>> F = coulombf >>> G = coulombg >>> for z in [3.5, -1, 2+3j]: ... chop(F(l-1,eta,z)*G(l,eta,z)-F(l,eta,z)*G(l-1,eta,z) - l/sqrt(l**2+eta**2)) ... 0.0 0.0 0.0
An integral identity connecting the regular and irregular wave functions:
>>> l, eta, z = 4+j, 2-j, 5+2j >>> coulombf(l,eta,z) + j*coulombg(l,eta,z) (0.7997977752284033239714479 + 0.9294486669502295512503127j) >>> g = lambda t: exp(-t)*t**(l-j*eta)*(t+2*j*z)**(l+j*eta) >>> j*exp(-j*z)*z**(-l)/fac(2*l+1)/coulombc(l,eta)*quad(g, [0,inf]) (0.7997977752284033239714479 + 0.9294486669502295512503127j)
Some test case with complex parameters, taken from Michel [2]:
>>> mp.dps = 15 >>> coulombf(1+0.1j, 50+50j, 100.156) (-1.02107292320897e+15 - 2.83675545731519e+15j) >>> coulombg(1+0.1j, 50+50j, 100.156) (2.83675545731519e+15 - 1.02107292320897e+15j) >>> coulombf(1e-5j, 10+1e-5j, 0.1+1e-6j) (4.30566371247811e-14 - 9.03347835361657e-19j) >>> coulombg(1e-5j, 10+1e-5j, 0.1+1e-6j) (778709182061.134 + 18418936.2660553j)
The following reproduces a table in Abramowitz & Stegun, at twice the precision:
>>> mp.dps = 10 >>> eta = 2; z = 5 >>> for l in [5, 4, 3, 2, 1, 0]: ... print("%s %s %s" % (l, coulombf(l,eta,z), ... diff(lambda z: coulombf(l,eta,z), z))) ... 5 0.09079533488 0.1042553261 4 0.2148205331 0.2029591779 3 0.4313159311 0.320534053 2 0.7212774133 0.3952408216 1 0.9935056752 0.3708676452 0 1.143337392 0.2937960375
References
I.J. Thompson & A.R. Barnett, “Coulomb and Bessel Functions of Complex Arguments and Order”, J. Comp. Phys., vol 64, no. 2, June 1986.
N. Michel, “Precise Coulomb wave functions for a wide range of complex \(l\), \(\eta\) and \(z\)”, http://arxiv.org/abs/physics/0702051v1
coulombg()¶
- mpmath.coulombg(l, eta, z)¶
Calculates the irregular Coulomb wave function
\[G_l(\eta,z) = \frac{F_l(\eta,z) \cos(\chi) - F_{-l-1}(\eta,z)}{\sin(\chi)}\]where \(\chi = \sigma_l - \sigma_{-l-1} - (l+1/2) \pi\) and \(\sigma_l(\eta) = (\ln \Gamma(1+l+i\eta)-\ln \Gamma(1+l-i\eta))/(2i)\).
See
coulombf()for additional information.Plots
# Irregular Coulomb wave functions -- equivalent to figure 14.5 in A&S F1 = lambda x: coulombg(0,0,x) F2 = lambda x: coulombg(0,1,x) F3 = lambda x: coulombg(0,5,x) F4 = lambda x: coulombg(0,10,x) F5 = lambda x: coulombg(0,x/2,x) plot([F1,F2,F3,F4,F5], [0,30], [-2,2])
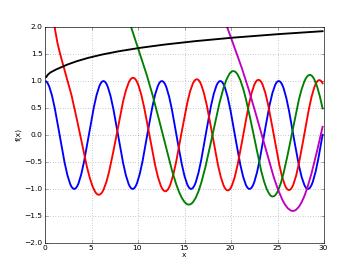
# Irregular Coulomb wave function in the complex plane cplot(lambda z: coulombg(1,1,z), points=50000)
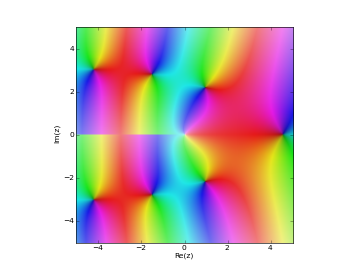
Examples
Evaluation is supported for arbitrary magnitudes of \(z\):
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> coulombg(-2, 1.5, 3.5) 1.380011900612186346255524 >>> coulombg(2, 1.5, 3.5) 1.919153700722748795245926 >>> coulombg(-2, 1.5, '1e-10') 201126715824.7329115106793 >>> coulombg(-2, 1.5, 1000) 0.1802071520691149410425512 >>> coulombg(-2, 1.5, 10**10) 0.652103020061678070929794
The following reproduces a table in Abramowitz & Stegun, at twice the precision:
>>> mp.dps = 10 >>> eta = 2; z = 5 >>> for l in [1, 2, 3, 4, 5]: ... print("%s %s %s" % (l, coulombg(l,eta,z), ... -diff(lambda z: coulombg(l,eta,z), z))) ... 1 1.08148276 0.6028279961 2 1.496877075 0.5661803178 3 2.048694714 0.7959909551 4 3.09408669 1.731802374 5 5.629840456 4.549343289
Evaluation close to the singularity at \(z = 0\):
>>> mp.dps = 15 >>> coulombg(0,10,1) 3088184933.67358 >>> coulombg(0,10,'1e-10') 5554866000719.8 >>> coulombg(0,10,'1e-100') 5554866221524.1
Evaluation with a half-integer value for \(l\):
>>> coulombg(1.5, 1, 10) 0.852320038297334
coulombc()¶
- mpmath.coulombc(l, eta)¶
Gives the normalizing Gamow constant for Coulomb wave functions,
\[C_l(\eta) = 2^l \exp\left(-\pi \eta/2 + [\ln \Gamma(1+l+i\eta) + \ln \Gamma(1+l-i\eta)]/2 - \ln \Gamma(2l+2)\right),\]where the log gamma function with continuous imaginary part away from the negative half axis (see
loggamma()) is implied.This function is used internally for the calculation of Coulomb wave functions, and automatically cached to make multiple evaluations with fixed \(l\), \(\eta\) fast.
Confluent U and Whittaker functions¶
hyperu()¶
- mpmath.hyperu(a, b, z)¶
Gives the Tricomi confluent hypergeometric function \(U\), also known as the Kummer or confluent hypergeometric function of the second kind. This function gives a second linearly independent solution to the confluent hypergeometric differential equation (the first is provided by \(\,_1F_1\) – see
hyp1f1()).Examples
Evaluation for arbitrary complex arguments:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> hyperu(2,3,4) 0.0625 >>> hyperu(0.25, 5, 1000) 0.1779949416140579573763523 >>> hyperu(0.25, 5, -1000) (0.1256256609322773150118907 - 0.1256256609322773150118907j)
The \(U\) function may be singular at \(z = 0\):
>>> hyperu(1.5, 2, 0) +inf >>> hyperu(1.5, -2, 0) 0.1719434921288400112603671
Verifying the differential equation:
>>> a, b = 1.5, 2 >>> f = lambda z: hyperu(a,b,z) >>> for z in [-10, 3, 3+4j]: ... chop(z*diff(f,z,2) + (b-z)*diff(f,z) - a*f(z)) ... 0.0 0.0 0.0
An integral representation:
>>> a,b,z = 2, 3.5, 4.25 >>> hyperu(a,b,z) 0.06674960718150520648014567 >>> quad(lambda t: exp(-z*t)*t**(a-1)*(1+t)**(b-a-1),[0,inf]) / gamma(a) 0.06674960718150520648014567
whitm()¶
- mpmath.whitm(k, m, z)¶
Evaluates the Whittaker function \(M(k,m,z)\), which gives a solution to the Whittaker differential equation
\[\frac{d^2f}{dz^2} + \left(-\frac{1}{4}+\frac{k}{z}+ \frac{(\frac{1}{4}-m^2)}{z^2}\right) f = 0.\]A second solution is given by
whitw().The Whittaker functions are defined in Abramowitz & Stegun, section 13.1. They are alternate forms of the confluent hypergeometric functions \(\,_1F_1\) and \(U\):
\[ \begin{align}\begin{aligned}M(k,m,z) = e^{-\frac{1}{2}z} z^{\frac{1}{2}+m} \,_1F_1(\tfrac{1}{2}+m-k, 1+2m, z)\\W(k,m,z) = e^{-\frac{1}{2}z} z^{\frac{1}{2}+m} U(\tfrac{1}{2}+m-k, 1+2m, z).\end{aligned}\end{align} \]Examples
Evaluation for arbitrary real and complex arguments is supported:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> whitm(1, 1, 1) 0.7302596799460411820509668 >>> whitm(1, 1, -1) (0.0 - 1.417977827655098025684246j) >>> whitm(j, j/2, 2+3j) (3.245477713363581112736478 - 0.822879187542699127327782j) >>> whitm(2, 3, 100000) 4.303985255686378497193063e+21707
Evaluation at zero:
>>> whitm(1,-1,0); whitm(1,-0.5,0); whitm(1,0,0) +inf nan 0.0
We can verify that
whitm()numerically satisfies the differential equation for arbitrarily chosen values:>>> k = mpf(0.25) >>> m = mpf(1.5) >>> f = lambda z: whitm(k,m,z) >>> for z in [-1, 2.5, 3, 1+2j]: ... chop(diff(f,z,2) + (-0.25 + k/z + (0.25-m**2)/z**2)*f(z)) ... 0.0 0.0 0.0 0.0
An integral involving both
whitm()andwhitw(), verifying evaluation along the real axis:>>> quad(lambda x: exp(-x)*whitm(3,2,x)*whitw(1,-2,x), [0,inf]) 3.438869842576800225207341 >>> 128/(21*sqrt(pi)) 3.438869842576800225207341
whitw()¶
- mpmath.whitw(k, m, z)¶
Evaluates the Whittaker function \(W(k,m,z)\), which gives a second solution to the Whittaker differential equation. (See
whitm().)Examples
Evaluation for arbitrary real and complex arguments is supported:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> whitw(1, 1, 1) 1.19532063107581155661012 >>> whitw(1, 1, -1) (-0.9424875979222187313924639 - 0.2607738054097702293308689j) >>> whitw(j, j/2, 2+3j) (0.1782899315111033879430369 - 0.01609578360403649340169406j) >>> whitw(2, 3, 100000) 1.887705114889527446891274e-21705 >>> whitw(-1, -1, 100) 1.905250692824046162462058e-24
Evaluation at zero:
>>> for m in [-1, -0.5, 0, 0.5, 1]: ... whitw(1, m, 0) ... +inf nan 0.0 nan +inf
We can verify that
whitw()numerically satisfies the differential equation for arbitrarily chosen values:>>> k = mpf(0.25) >>> m = mpf(1.5) >>> f = lambda z: whitw(k,m,z) >>> for z in [-1, 2.5, 3, 1+2j]: ... chop(diff(f,z,2) + (-0.25 + k/z + (0.25-m**2)/z**2)*f(z)) ... 0.0 0.0 0.0 0.0
Parabolic cylinder functions¶
pcfd()¶
- mpmath.pcfd(n, z, **kwargs)¶
Gives the parabolic cylinder function in Whittaker’s notation \(D_n(z) = U(-n-1/2, z)\) (see
pcfu()). It solves the differential equation\[y'' + \left(n + \frac{1}{2} - \frac{1}{4} z^2\right) y = 0.\]and can be represented in terms of Hermite polynomials (see
hermite()) as\[D_n(z) = 2^{-n/2} e^{-z^2/4} H_n\left(\frac{z}{\sqrt{2}}\right).\]Plots
# Parabolic cylinder function D_n(x) on the real line for n=0,1,2,3,4 d0 = lambda x: pcfd(0,x) d1 = lambda x: pcfd(1,x) d2 = lambda x: pcfd(2,x) d3 = lambda x: pcfd(3,x) d4 = lambda x: pcfd(4,x) plot([d0,d1,d2,d3,d4],[-7,7])
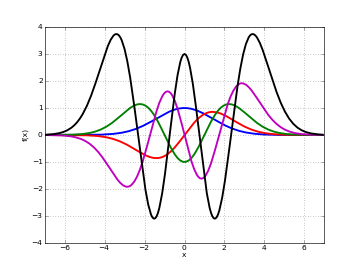
Examples
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> pcfd(0,0); pcfd(1,0); pcfd(2,0); pcfd(3,0) 1.0 0.0 -1.0 0.0 >>> pcfd(4,0); pcfd(-3,0) 3.0 0.6266570686577501256039413 >>> pcfd('1/2', 2+3j) (-5.363331161232920734849056 - 3.858877821790010714163487j) >>> pcfd(2, -10) 1.374906442631438038871515e-9
Verifying the differential equation:
>>> n = mpf(2.5) >>> y = lambda z: pcfd(n,z) >>> z = 1.75 >>> chop(diff(y,z,2) + (n+0.5-0.25*z**2)*y(z)) 0.0
Rational Taylor series expansion when \(n\) is an integer:
>>> taylor(lambda z: pcfd(5,z), 0, 7) [0.0, 15.0, 0.0, -13.75, 0.0, 3.96875, 0.0, -0.6015625]
pcfu()¶
- mpmath.pcfu(a, z, **kwargs)¶
Gives the parabolic cylinder function \(U(a,z)\), which may be defined for \(\Re(z) > 0\) in terms of the confluent U-function (see
hyperu()) by\[U(a,z) = 2^{-\frac{1}{4}-\frac{a}{2}} e^{-\frac{1}{4} z^2} U\left(\frac{a}{2}+\frac{1}{4}, \frac{1}{2}, \frac{1}{2}z^2\right)\]or, for arbitrary \(z\),
\[e^{-\frac{1}{4}z^2} U(a,z) = U(a,0) \,_1F_1\left(-\tfrac{a}{2}+\tfrac{1}{4}; \tfrac{1}{2}; -\tfrac{1}{2}z^2\right) + U'(a,0) z \,_1F_1\left(-\tfrac{a}{2}+\tfrac{3}{4}; \tfrac{3}{2}; -\tfrac{1}{2}z^2\right).\]Examples
Connection to other functions:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> z = mpf(3) >>> pcfu(0.5,z) 0.03210358129311151450551963 >>> sqrt(pi/2)*exp(z**2/4)*erfc(z/sqrt(2)) 0.03210358129311151450551963 >>> pcfu(0.5,-z) 23.75012332835297233711255 >>> sqrt(pi/2)*exp(z**2/4)*erfc(-z/sqrt(2)) 23.75012332835297233711255 >>> pcfu(0.5,-z) 23.75012332835297233711255 >>> sqrt(pi/2)*exp(z**2/4)*erfc(-z/sqrt(2)) 23.75012332835297233711255
pcfv()¶
- mpmath.pcfv(a, z, **kwargs)¶
Gives the parabolic cylinder function \(V(a,z)\), which can be represented in terms of
pcfu()as\[V(a,z) = \frac{\Gamma(a+\tfrac{1}{2}) (U(a,-z)-\sin(\pi a) U(a,z)}{\pi}.\]Examples
Wronskian relation between \(U\) and \(V\):
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> a, z = 2, 3 >>> pcfu(a,z)*diff(pcfv,(a,z),(0,1))-diff(pcfu,(a,z),(0,1))*pcfv(a,z) 0.7978845608028653558798921 >>> sqrt(2/pi) 0.7978845608028653558798921 >>> a, z = 2.5, 3 >>> pcfu(a,z)*diff(pcfv,(a,z),(0,1))-diff(pcfu,(a,z),(0,1))*pcfv(a,z) 0.7978845608028653558798921 >>> a, z = 0.25, -1 >>> pcfu(a,z)*diff(pcfv,(a,z),(0,1))-diff(pcfu,(a,z),(0,1))*pcfv(a,z) 0.7978845608028653558798921 >>> a, z = 2+1j, 2+3j >>> chop(pcfu(a,z)*diff(pcfv,(a,z),(0,1))-diff(pcfu,(a,z),(0,1))*pcfv(a,z)) 0.7978845608028653558798921
pcfw()¶
- mpmath.pcfw(a, z, **kwargs)¶
Gives the parabolic cylinder function \(W(a,z)\) defined in (DLMF 12.14).
Examples
Value at the origin:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> a = mpf(0.25) >>> pcfw(a,0) 0.9722833245718180765617104 >>> power(2,-0.75)*sqrt(abs(gamma(0.25+0.5j*a)/gamma(0.75+0.5j*a))) 0.9722833245718180765617104 >>> diff(pcfw,(a,0),(0,1)) -0.5142533944210078966003624 >>> -power(2,-0.25)*sqrt(abs(gamma(0.75+0.5j*a)/gamma(0.25+0.5j*a))) -0.5142533944210078966003624