Zeta functions, L-series and polylogarithms¶
This section includes the Riemann zeta functions and associated functions pertaining to analytic number theory.
Riemann and Hurwitz zeta functions¶
zeta()¶
- mpmath.zeta(s, a=1, derivative=0)¶
Computes the Riemann zeta function

or, with
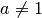 , the more general Hurwitz zeta function
, the more general Hurwitz zeta function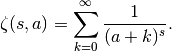
Optionally, zeta(s, a, n) computes the
 -th derivative with
respect to
-th derivative with
respect to  ,
,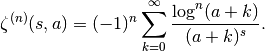
Although these series only converge for
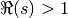 , the Riemann and Hurwitz
zeta functions are defined through analytic continuation for arbitrary
complex
, the Riemann and Hurwitz
zeta functions are defined through analytic continuation for arbitrary
complex 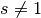 (
(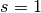 is a pole).
is a pole).The implementation uses three algorithms: the Borwein algorithm for the Riemann zeta function when
 is close to the real line;
the Riemann-Siegel formula for the Riemann zeta function when
is close to the real line;
the Riemann-Siegel formula for the Riemann zeta function when  is
large imaginary, and Euler-Maclaurin summation in all other cases.
The reflection formula for
is
large imaginary, and Euler-Maclaurin summation in all other cases.
The reflection formula for 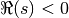 is implemented in some cases.
The algorithm can be chosen with method = 'borwein',
method='riemann-siegel' or method = 'euler-maclaurin'.
is implemented in some cases.
The algorithm can be chosen with method = 'borwein',
method='riemann-siegel' or method = 'euler-maclaurin'.The parameter
 is usually a rational number
is usually a rational number 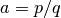 , and may be specified
as such by passing an integer tuple
, and may be specified
as such by passing an integer tuple 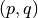 . Evaluation is supported for
arbitrary complex
. Evaluation is supported for
arbitrary complex  , but may be slow and/or inaccurate when
, but may be slow and/or inaccurate when 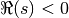 for
nonrational
for
nonrational  or when computing derivatives.
or when computing derivatives.Examples
Some values of the Riemann zeta function:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> zeta(2); pi**2 / 6 1.644934066848226436472415 1.644934066848226436472415 >>> zeta(0) -0.5 >>> zeta(-1) -0.08333333333333333333333333 >>> zeta(-2) 0.0
For large positive
 ,
, 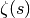 rapidly approaches 1:
rapidly approaches 1:>>> zeta(50) 1.000000000000000888178421 >>> zeta(100) 1.0 >>> zeta(inf) 1.0 >>> 1-sum((zeta(k)-1)/k for k in range(2,85)); +euler 0.5772156649015328606065121 0.5772156649015328606065121 >>> nsum(lambda k: zeta(k)-1, [2, inf]) 1.0
Evaluation is supported for complex
 and
and  :
:>>> zeta(-3+4j) (-0.03373057338827757067584698 + 0.2774499251557093745297677j) >>> zeta(2+3j, -1+j) (389.6841230140842816370741 + 295.2674610150305334025962j)
The Riemann zeta function has so-called nontrivial zeros on the critical line
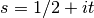 :
:>>> findroot(zeta, 0.5+14j); zetazero(1) (0.5 + 14.13472514173469379045725j) (0.5 + 14.13472514173469379045725j) >>> findroot(zeta, 0.5+21j); zetazero(2) (0.5 + 21.02203963877155499262848j) (0.5 + 21.02203963877155499262848j) >>> findroot(zeta, 0.5+25j); zetazero(3) (0.5 + 25.01085758014568876321379j) (0.5 + 25.01085758014568876321379j) >>> chop(zeta(zetazero(10))) 0.0
Evaluation on and near the critical line is supported for large heights
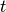 by means of the Riemann-Siegel formula (currently
for
by means of the Riemann-Siegel formula (currently
for 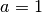 ,
, 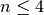 ):
):>>> zeta(0.5+100000j) (1.073032014857753132114076 + 5.780848544363503984261041j) >>> zeta(0.75+1000000j) (0.9535316058375145020351559 + 0.9525945894834273060175651j) >>> zeta(0.5+10000000j) (11.45804061057709254500227 - 8.643437226836021723818215j) >>> zeta(0.5+100000000j, derivative=1) (51.12433106710194942681869 + 43.87221167872304520599418j) >>> zeta(0.5+100000000j, derivative=2) (-444.2760822795430400549229 - 896.3789978119185981665403j) >>> zeta(0.5+100000000j, derivative=3) (3230.72682687670422215339 + 14374.36950073615897616781j) >>> zeta(0.5+100000000j, derivative=4) (-11967.35573095046402130602 - 218945.7817789262839266148j) >>> zeta(1+10000000j) # off the line (2.859846483332530337008882 + 0.491808047480981808903986j) >>> zeta(1+10000000j, derivative=1) (-4.333835494679647915673205 - 0.08405337962602933636096103j) >>> zeta(1+10000000j, derivative=4) (453.2764822702057701894278 - 581.963625832768189140995j)
For investigation of the zeta function zeros, the Riemann-Siegel Z-function is often more convenient than working with the Riemann zeta function directly (see siegelz()).
Some values of the Hurwitz zeta function:
>>> zeta(2, 3); -5./4 + pi**2/6 0.3949340668482264364724152 0.3949340668482264364724152 >>> zeta(2, (3,4)); pi**2 - 8*catalan 2.541879647671606498397663 2.541879647671606498397663
For positive integer values of
 , the Hurwitz zeta function is
equivalent to a polygamma function (except for a normalizing factor):
, the Hurwitz zeta function is
equivalent to a polygamma function (except for a normalizing factor):>>> zeta(4, (1,5)); psi(3, '1/5')/6 625.5408324774542966919938 625.5408324774542966919938
Evaluation of derivatives:
>>> zeta(0, 3+4j, 1); loggamma(3+4j) - ln(2*pi)/2 (-2.675565317808456852310934 + 4.742664438034657928194889j) (-2.675565317808456852310934 + 4.742664438034657928194889j) >>> zeta(2, 1, 20) 2432902008176640000.000242 >>> zeta(3+4j, 5.5+2j, 4) (-0.140075548947797130681075 - 0.3109263360275413251313634j) >>> zeta(0.5+100000j, 1, 4) (-10407.16081931495861539236 + 13777.78669862804508537384j) >>> zeta(-100+0.5j, (1,3), derivative=4) (4.007180821099823942702249e+79 + 4.916117957092593868321778e+78j)
Generating a Taylor series at
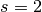 using derivatives:
using derivatives:>>> for k in range(11): print("%s * (s-2)^%i" % (zeta(2,1,k)/fac(k), k)) ... 1.644934066848226436472415 * (s-2)^0 -0.9375482543158437537025741 * (s-2)^1 0.9946401171494505117104293 * (s-2)^2 -1.000024300473840810940657 * (s-2)^3 1.000061933072352565457512 * (s-2)^4 -1.000006869443931806408941 * (s-2)^5 1.000000173233769531820592 * (s-2)^6 -0.9999999569989868493432399 * (s-2)^7 0.9999999937218844508684206 * (s-2)^8 -0.9999999996355013916608284 * (s-2)^9 1.000000000004610645020747 * (s-2)^10
Evaluation at zero and for negative integer
 :
:>>> zeta(0, 10) -9.5 >>> zeta(-2, (2,3)); mpf(1)/81 0.01234567901234567901234568 0.01234567901234567901234568 >>> zeta(-3+4j, (5,4)) (0.2899236037682695182085988 + 0.06561206166091757973112783j) >>> zeta(-3.25, 1/pi) -0.0005117269627574430494396877 >>> zeta(-3.5, pi, 1) 11.156360390440003294709 >>> zeta(-100.5, (8,3)) -4.68162300487989766727122e+77 >>> zeta(-10.5, (-8,3)) (-0.01521913704446246609237979 + 29907.72510874248161608216j) >>> zeta(-1000.5, (-8,3)) (1.031911949062334538202567e+1770 + 1.519555750556794218804724e+426j) >>> zeta(-1+j, 3+4j) (-16.32988355630802510888631 - 22.17706465801374033261383j) >>> zeta(-1+j, 3+4j, 2) (32.48985276392056641594055 - 51.11604466157397267043655j) >>> diff(lambda s: zeta(s, 3+4j), -1+j, 2) (32.48985276392056641594055 - 51.11604466157397267043655j)
References
Dirichlet L-series¶
altzeta()¶
- mpmath.altzeta(s)¶
Gives the Dirichlet eta function,
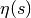 , also known as the
alternating zeta function. This function is defined in analogy
with the Riemann zeta function as providing the sum of the
alternating series
, also known as the
alternating zeta function. This function is defined in analogy
with the Riemann zeta function as providing the sum of the
alternating series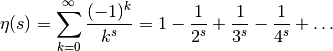
The eta function, unlike the Riemann zeta function, is an entire function, having a finite value for all complex
 . The special case
. The special case
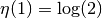 gives the value of the alternating harmonic series.
gives the value of the alternating harmonic series.The alternating zeta function may expressed using the Riemann zeta function as
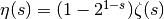 . It can also be expressed
in terms of the Hurwitz zeta function, for example using
dirichlet() (see documentation for that function).
. It can also be expressed
in terms of the Hurwitz zeta function, for example using
dirichlet() (see documentation for that function).Examples
Some special values are:
>>> from mpmath import * >>> mp.dps = 15; mp.pretty = True >>> altzeta(1) 0.693147180559945 >>> altzeta(0) 0.5 >>> altzeta(-1) 0.25 >>> altzeta(-2) 0.0
An example of a sum that can be computed more accurately and efficiently via altzeta() than via numerical summation:
>>> sum(-(-1)**n / mpf(n)**2.5 for n in range(1, 100)) 0.867204951503984 >>> altzeta(2.5) 0.867199889012184
At positive even integers, the Dirichlet eta function evaluates to a rational multiple of a power of
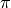 :
:>>> altzeta(2) 0.822467033424113 >>> pi**2/12 0.822467033424113
Like the Riemann zeta function,
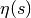 , approaches 1
as
, approaches 1
as  approaches positive infinity, although it does
so from below rather than from above:
approaches positive infinity, although it does
so from below rather than from above:>>> altzeta(30) 0.999999999068682 >>> altzeta(inf) 1.0 >>> mp.pretty = False >>> altzeta(1000, rounding='d') mpf('0.99999999999999989') >>> altzeta(1000, rounding='u') mpf('1.0')
References
dirichlet()¶
- mpmath.dirichlet(s, chi, derivative=0)¶
Evaluates the Dirichlet L-function
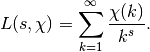
where
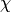 is a periodic sequence of length
is a periodic sequence of length 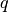 which should be supplied
in the form of a list
which should be supplied
in the form of a list ![[\chi(0), \chi(1), \ldots, \chi(q-1)]](../_images/math/7f94c0f2abbb6e9220f8c347445a68b404f0a915.png) .
Strictly,
.
Strictly, 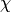 should be a Dirichlet character, but any periodic
sequence will work.
should be a Dirichlet character, but any periodic
sequence will work.For example, dirichlet(s, [1]) gives the ordinary Riemann zeta function and dirichlet(s, [-1,1]) gives the alternating zeta function (Dirichlet eta function).
Also the derivative with respect to
 (currently only a first
derivative) can be evaluated.
(currently only a first
derivative) can be evaluated.Examples
The ordinary Riemann zeta function:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> dirichlet(3, [1]); zeta(3) 1.202056903159594285399738 1.202056903159594285399738 >>> dirichlet(1, [1]) +inf
The alternating zeta function:
>>> dirichlet(1, [-1,1]); ln(2) 0.6931471805599453094172321 0.6931471805599453094172321
The following defines the Dirichlet beta function
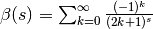 and verifies
several values of this function:
and verifies
several values of this function:>>> B = lambda s, d=0: dirichlet(s, [0, 1, 0, -1], d) >>> B(0); 1./2 0.5 0.5 >>> B(1); pi/4 0.7853981633974483096156609 0.7853981633974483096156609 >>> B(2); +catalan 0.9159655941772190150546035 0.9159655941772190150546035 >>> B(2,1); diff(B, 2) 0.08158073611659279510291217 0.08158073611659279510291217 >>> B(-1,1); 2*catalan/pi 0.5831218080616375602767689 0.5831218080616375602767689 >>> B(0,1); log(gamma(0.25)**2/(2*pi*sqrt(2))) 0.3915943927068367764719453 0.3915943927068367764719454 >>> B(1,1); 0.25*pi*(euler+2*ln2+3*ln(pi)-4*ln(gamma(0.25))) 0.1929013167969124293631898 0.1929013167969124293631898
A custom L-series of period 3:
>>> dirichlet(2, [2,0,1]) 0.7059715047839078092146831 >>> 2*nsum(lambda k: (3*k)**-2, [1,inf]) + \ ... nsum(lambda k: (3*k+2)**-2, [0,inf]) 0.7059715047839078092146831
Stieltjes constants¶
stieltjes()¶
- mpmath.stieltjes(n, a=1)¶
For a nonnegative integer
 , stieltjes(n) computes the
, stieltjes(n) computes the
 -th Stieltjes constant
-th Stieltjes constant 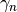 , defined as the
, defined as the
 -th coefficient in the Laurent series expansion of the
Riemann zeta function around the pole at
-th coefficient in the Laurent series expansion of the
Riemann zeta function around the pole at 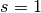 . That is,
we have:
. That is,
we have: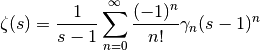
More generally, stieltjes(n, a) gives the corresponding coefficient
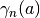 for the Hurwitz zeta function
for the Hurwitz zeta function
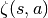 (with
(with 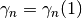 ).
).Examples
The zeroth Stieltjes constant is just Euler’s constant
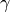 :
:>>> from mpmath import * >>> mp.dps = 15; mp.pretty = True >>> stieltjes(0) 0.577215664901533
Some more values are:
>>> stieltjes(1) -0.0728158454836767 >>> stieltjes(10) 0.000205332814909065 >>> stieltjes(30) 0.00355772885557316 >>> stieltjes(1000) -1.57095384420474e+486 >>> stieltjes(2000) 2.680424678918e+1109 >>> stieltjes(1, 2.5) -0.23747539175716
An alternative way to compute
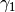 :
:>>> diff(extradps(15)(lambda x: 1/(x-1) - zeta(x)), 1) -0.0728158454836767
stieltjes() supports arbitrary precision evaluation:
>>> mp.dps = 50 >>> stieltjes(2) -0.0096903631928723184845303860352125293590658061013408
Algorithm
stieltjes() numerically evaluates the integral in the following representation due to Ainsworth, Howell and Coffey [1], [2]:
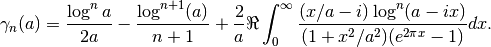
For some reference values with
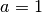 , see e.g. [4].
, see e.g. [4].References
- O. R. Ainsworth & L. W. Howell, “An integral representation of the generalized Euler-Mascheroni constants”, NASA Technical Paper 2456 (1985), http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19850014994_1985014994.pdf
- M. W. Coffey, “The Stieltjes constants, their relation to the
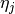 coefficients, and representation of the Hurwitz
zeta function”, arXiv:0706.0343v1 http://arxiv.org/abs/0706.0343
coefficients, and representation of the Hurwitz
zeta function”, arXiv:0706.0343v1 http://arxiv.org/abs/0706.0343 - http://mathworld.wolfram.com/StieltjesConstants.html
- http://pi.lacim.uqam.ca/piDATA/stieltjesgamma.txt
Zeta function zeros¶
These functions are used for the study of the Riemann zeta function in the critical strip.
zetazero()¶
- mpmath.zetazero(n, verbose=False)¶
Computes the
 -th nontrivial zero of
-th nontrivial zero of 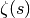 on the critical line,
i.e. returns an approximation of the
on the critical line,
i.e. returns an approximation of the  -th largest complex number
-th largest complex number
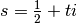 for which
for which 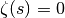 . Equivalently, the
imaginary part
. Equivalently, the
imaginary part 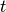 is a zero of the Z-function (siegelz()).
is a zero of the Z-function (siegelz()).Examples
The first few zeros:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> zetazero(1) (0.5 + 14.13472514173469379045725j) >>> zetazero(2) (0.5 + 21.02203963877155499262848j) >>> zetazero(20) (0.5 + 77.14484006887480537268266j)
Verifying that the values are zeros:
>>> for n in range(1,5): ... s = zetazero(n) ... chop(zeta(s)), chop(siegelz(s.imag)) ... (0.0, 0.0) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0)
Negative indices give the conjugate zeros (
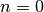 is undefined):
is undefined):>>> zetazero(-1) (0.5 - 14.13472514173469379045725j)
zetazero() supports arbitrarily large
 and arbitrary precision:
and arbitrary precision:>>> mp.dps = 15 >>> zetazero(1234567) (0.5 + 727690.906948208j) >>> mp.dps = 50 >>> zetazero(1234567) (0.5 + 727690.9069482075392389420041147142092708393819935j) >>> chop(zeta(_)/_) 0.0
with info=True, zetazero() gives additional information:
>>> mp.dps = 15 >>> zetazero(542964976,info=True) ((0.5 + 209039046.578535j), [542964969, 542964978], 6, '(013111110)')
This means that the zero is between Gram points 542964969 and 542964978; it is the 6-th zero between them. Finally (01311110) is the pattern of zeros in this interval. The numbers indicate the number of zeros in each Gram interval (Rosser blocks between parenthesis). In this case there is only one Rosser block of length nine.
nzeros()¶
- mpmath.nzeros(t)¶
Computes the number of zeros of the Riemann zeta function in
![(0,1) \times (0,t]](../_images/math/34f0c1aac73e7421181d7980e6acfd3520964bef.png) , usually denoted by
, usually denoted by 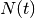 .
.Examples
The first zero has imaginary part between 14 and 15:
>>> from mpmath import * >>> mp.dps = 15; mp.pretty = True >>> nzeros(14) 0 >>> nzeros(15) 1 >>> zetazero(1) (0.5 + 14.1347251417347j)
Some closely spaced zeros:
>>> nzeros(10**7) 21136125 >>> zetazero(21136125) (0.5 + 9999999.32718175j) >>> zetazero(21136126) (0.5 + 10000000.2400236j) >>> nzeros(545439823.215) 1500000001 >>> zetazero(1500000001) (0.5 + 545439823.201985j) >>> zetazero(1500000002) (0.5 + 545439823.325697j)
This confirms the data given by J. van de Lune, H. J. J. te Riele and D. T. Winter in 1986.
siegelz()¶
- mpmath.siegelz(t)¶
Computes the Z-function, also known as the Riemann-Siegel Z function,
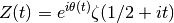
where
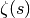 is the Riemann zeta function (zeta())
and where
is the Riemann zeta function (zeta())
and where 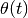 denotes the Riemann-Siegel theta function
(see siegeltheta()).
denotes the Riemann-Siegel theta function
(see siegeltheta()).Evaluation is supported for real and complex arguments:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> siegelz(1) -0.7363054628673177346778998 >>> siegelz(3+4j) (-0.1852895764366314976003936 - 0.2773099198055652246992479j)
The first four derivatives are supported, using the optional derivative keyword argument:
>>> siegelz(1234567, derivative=3) 56.89689348495089294249178 >>> diff(siegelz, 1234567, n=3) 56.89689348495089294249178
The Z-function has a Maclaurin expansion:
>>> nprint(chop(taylor(siegelz, 0, 4))) [-1.46035, 0.0, 2.73588, 0.0, -8.39357]
The Z-function
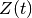 is equal to
is equal to 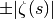 on the
critical line
on the
critical line 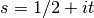 (i.e. for real arguments
(i.e. for real arguments 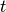 to
to 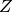 ). Its zeros coincide with those of the Riemann zeta
function:
). Its zeros coincide with those of the Riemann zeta
function:>>> findroot(siegelz, 14) 14.13472514173469379045725 >>> findroot(siegelz, 20) 21.02203963877155499262848 >>> findroot(zeta, 0.5+14j) (0.5 + 14.13472514173469379045725j) >>> findroot(zeta, 0.5+20j) (0.5 + 21.02203963877155499262848j)
Since the Z-function is real-valued on the critical line (and unlike
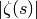 analytic), it is useful for
investigating the zeros of the Riemann zeta function.
For example, one can use a root-finding algorithm based
on sign changes:
analytic), it is useful for
investigating the zeros of the Riemann zeta function.
For example, one can use a root-finding algorithm based
on sign changes:>>> findroot(siegelz, [100, 200], solver='bisect') 176.4414342977104188888926
To locate roots, Gram points
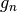 which can be computed
by grampoint() are useful. If
which can be computed
by grampoint() are useful. If 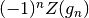 is
positive for two consecutive
is
positive for two consecutive  , then
, then 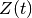 must have
a zero between those points:
must have
a zero between those points:>>> g10 = grampoint(10) >>> g11 = grampoint(11) >>> (-1)**10 * siegelz(g10) > 0 True >>> (-1)**11 * siegelz(g11) > 0 True >>> findroot(siegelz, [g10, g11], solver='bisect') 56.44624769706339480436776 >>> g10, g11 (54.67523744685325626632663, 57.54516517954725443703014)
siegeltheta()¶
- mpmath.siegeltheta(t)¶
Computes the Riemann-Siegel theta function,
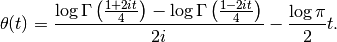
The Riemann-Siegel theta function is important in providing the phase factor for the Z-function (see siegelz()). Evaluation is supported for real and complex arguments:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> siegeltheta(0) 0.0 >>> siegeltheta(inf) +inf >>> siegeltheta(-inf) -inf >>> siegeltheta(1) -1.767547952812290388302216 >>> siegeltheta(10+0.25j) (-3.068638039426838572528867 + 0.05804937947429712998395177j)
Arbitrary derivatives may be computed with derivative = k
>>> siegeltheta(1234, derivative=2) 0.0004051864079114053109473741 >>> diff(siegeltheta, 1234, n=2) 0.0004051864079114053109473741
The Riemann-Siegel theta function has odd symmetry around
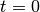 ,
two local extreme points and three real roots including 0 (located
symmetrically):
,
two local extreme points and three real roots including 0 (located
symmetrically):>>> nprint(chop(taylor(siegeltheta, 0, 5))) [0.0, -2.68609, 0.0, 2.69433, 0.0, -6.40218] >>> findroot(diffun(siegeltheta), 7) 6.28983598883690277966509 >>> findroot(siegeltheta, 20) 17.84559954041086081682634
For large
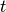 , there is a famous asymptotic formula
for
, there is a famous asymptotic formula
for 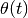 , to first order given by:
, to first order given by:>>> t = mpf(10**6) >>> siegeltheta(t) 5488816.353078403444882823 >>> -t*log(2*pi/t)/2-t/2 5488816.745777464310273645
grampoint()¶
- mpmath.grampoint(n)¶
Gives the
 -th Gram point
-th Gram point 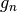 , defined as the solution
to the equation
, defined as the solution
to the equation 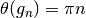 where
where 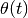 is the Riemann-Siegel theta function (siegeltheta()).
is the Riemann-Siegel theta function (siegeltheta()).The first few Gram points are:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> grampoint(0) 17.84559954041086081682634 >>> grampoint(1) 23.17028270124630927899664 >>> grampoint(2) 27.67018221781633796093849 >>> grampoint(3) 31.71797995476405317955149
Checking the definition:
>>> siegeltheta(grampoint(3)) 9.42477796076937971538793 >>> 3*pi 9.42477796076937971538793
A large Gram point:
>>> grampoint(10**10) 3293531632.728335454561153
Gram points are useful when studying the Z-function (siegelz()). See the documentation of that function for additional examples.
grampoint() can solve the defining equation for nonintegral
 . There is a fixed point where
. There is a fixed point where 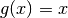 :
:>>> findroot(lambda x: grampoint(x) - x, 10000) 9146.698193171459265866198
References
backlunds()¶
- mpmath.backlunds(t)¶
Computes the function
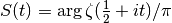 .
.See Titchmarsh Section 9.3 for details of the definition.
Examples
>>> from mpmath import * >>> mp.dps = 15; mp.pretty = True >>> backlunds(217.3) 0.16302205431184
Generally, the value is a small number. At Gram points it is an integer, frequently equal to 0:
>>> chop(backlunds(grampoint(200))) 0.0 >>> backlunds(extraprec(10)(grampoint)(211)) 1.0 >>> backlunds(extraprec(10)(grampoint)(232)) -1.0
The number of zeros of the Riemann zeta function up to height
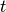 satisfies
satisfies 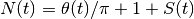 (see :func:nzeros` and
siegeltheta()):
(see :func:nzeros` and
siegeltheta()):>>> t = 1234.55 >>> nzeros(t) 842 >>> siegeltheta(t)/pi+1+backlunds(t) 842.0
Lerch transcendent¶
lerchphi()¶
- mpmath.lerchphi(z, s, a)¶
Gives the Lerch transcendent, defined for
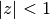 and
and
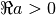 by
by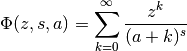
and generally by the recurrence
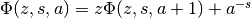 along with the integral representation valid for
along with the integral representation valid for 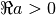
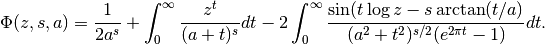
The Lerch transcendent generalizes the Hurwitz zeta function zeta() (
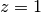 ) and the polylogarithm polylog() (
) and the polylogarithm polylog() (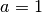 ).
).Examples
Several evaluations in terms of simpler functions:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> lerchphi(-1,2,0.5); 4*catalan 3.663862376708876060218414 3.663862376708876060218414 >>> diff(lerchphi, (-1,-2,1), (0,1,0)); 7*zeta(3)/(4*pi**2) 0.2131391994087528954617607 0.2131391994087528954617607 >>> lerchphi(-4,1,1); log(5)/4 0.4023594781085250936501898 0.4023594781085250936501898 >>> lerchphi(-3+2j,1,0.5); 2*atanh(sqrt(-3+2j))/sqrt(-3+2j) (1.142423447120257137774002 + 0.2118232380980201350495795j) (1.142423447120257137774002 + 0.2118232380980201350495795j)
Evaluation works for complex arguments and
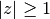 :
:>>> lerchphi(1+2j, 3-j, 4+2j) (0.002025009957009908600539469 + 0.003327897536813558807438089j) >>> lerchphi(-2,2,-2.5) -12.28676272353094275265944 >>> lerchphi(10,10,10) (-4.462130727102185701817349e-11 + 1.575172198981096218823481e-12j) >>> lerchphi(10,10,-10.5) (112658784011940.5605789002 + 498113185.5756221777743631j)
Some degenerate cases:
>>> lerchphi(0,1,2) 0.5 >>> lerchphi(0,1,-2) -0.5
Reduction to simpler functions:
>>> lerchphi(1, 4.25+1j, 1) (1.044674457556746668033975 - 0.04674508654012658932271226j) >>> zeta(4.25+1j) (1.044674457556746668033975 - 0.04674508654012658932271226j) >>> lerchphi(1 - 0.5**10, 4.25+1j, 1) (1.044629338021507546737197 - 0.04667768813963388181708101j) >>> lerchphi(3, 4, 1) (1.249503297023366545192592 - 0.2314252413375664776474462j) >>> polylog(4, 3) / 3 (1.249503297023366545192592 - 0.2314252413375664776474462j) >>> lerchphi(3, 4, 1 - 0.5**10) (1.253978063946663945672674 + 0.2316736622836535468765376j)
References
- [DLMF] section 25.14
Polylogarithms and Clausen functions¶
polylog()¶
- mpmath.polylog(s, z)¶
Computes the polylogarithm, defined by the sum
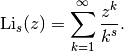
This series is convergent only for
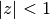 , so elsewhere
the analytic continuation is implied.
, so elsewhere
the analytic continuation is implied.The polylogarithm should not be confused with the logarithmic integral (also denoted by Li or li), which is implemented as li().
Examples
The polylogarithm satisfies a huge number of functional identities. A sample of polylogarithm evaluations is shown below:
>>> from mpmath import * >>> mp.dps = 15; mp.pretty = True >>> polylog(1,0.5), log(2) (0.693147180559945, 0.693147180559945) >>> polylog(2,0.5), (pi**2-6*log(2)**2)/12 (0.582240526465012, 0.582240526465012) >>> polylog(2,-phi), -log(phi)**2-pi**2/10 (-1.21852526068613, -1.21852526068613) >>> polylog(3,0.5), 7*zeta(3)/8-pi**2*log(2)/12+log(2)**3/6 (0.53721319360804, 0.53721319360804)
polylog() can evaluate the analytic continuation of the polylogarithm when
 is an integer:
is an integer:>>> polylog(2, 10) (0.536301287357863 - 7.23378441241546j) >>> polylog(2, -10) -4.1982778868581 >>> polylog(2, 10j) (-3.05968879432873 + 3.71678149306807j) >>> polylog(-2, 10) -0.150891632373114 >>> polylog(-2, -10) 0.067618332081142 >>> polylog(-2, 10j) (0.0384353698579347 + 0.0912451798066779j)
Some more examples, with arguments on the unit circle (note that the series definition cannot be used for computation here):
>>> polylog(2,j) (-0.205616758356028 + 0.915965594177219j) >>> j*catalan-pi**2/48 (-0.205616758356028 + 0.915965594177219j) >>> polylog(3,exp(2*pi*j/3)) (-0.534247512515375 + 0.765587078525922j) >>> -4*zeta(3)/9 + 2*j*pi**3/81 (-0.534247512515375 + 0.765587078525921j)
Polylogarithms of different order are related by integration and differentiation:
>>> s, z = 3, 0.5 >>> polylog(s+1, z) 0.517479061673899 >>> quad(lambda t: polylog(s,t)/t, [0, z]) 0.517479061673899 >>> z*diff(lambda t: polylog(s+2,t), z) 0.517479061673899
Taylor series expansions around
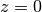 are:
are:>>> for n in range(-3, 4): ... nprint(taylor(lambda x: polylog(n,x), 0, 5)) ... [0.0, 1.0, 8.0, 27.0, 64.0, 125.0] [0.0, 1.0, 4.0, 9.0, 16.0, 25.0] [0.0, 1.0, 2.0, 3.0, 4.0, 5.0] [0.0, 1.0, 1.0, 1.0, 1.0, 1.0] [0.0, 1.0, 0.5, 0.333333, 0.25, 0.2] [0.0, 1.0, 0.25, 0.111111, 0.0625, 0.04] [0.0, 1.0, 0.125, 0.037037, 0.015625, 0.008]
The series defining the polylogarithm is simultaneously a Taylor series and an L-series. For certain values of
 , the
polylogarithm reduces to a pure zeta function:
, the
polylogarithm reduces to a pure zeta function:>>> polylog(pi, 1), zeta(pi) (1.17624173838258, 1.17624173838258) >>> polylog(pi, -1), -altzeta(pi) (-0.909670702980385, -0.909670702980385)
Evaluation for arbitrary, nonintegral
 is supported
for
is supported
for  within the unit circle:
within the unit circle:>>> polylog(3+4j, 0.25) (0.24258605789446 - 0.00222938275488344j) >>> nsum(lambda k: 0.25**k / k**(3+4j), [1,inf]) (0.24258605789446 - 0.00222938275488344j)
It is also currently supported outside of the unit circle for
 not too large in magnitude:
not too large in magnitude:>>> polylog(1+j, 20+40j) (-7.1421172179728 - 3.92726697721369j) >>> polylog(1+j, 200+400j) Traceback (most recent call last): ... NotImplementedError: polylog for arbitrary s and z
References
- Richard Crandall, “Note on fast polylogarithm computation” http://people.reed.edu/~crandall/papers/Polylog.pdf
- http://en.wikipedia.org/wiki/Polylogarithm
- http://mathworld.wolfram.com/Polylogarithm.html
clsin()¶
- mpmath.clsin(s, z)¶
Computes the Clausen sine function, defined formally by the series
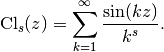
The special case
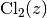 (i.e. clsin(2,z)) is the classical
“Clausen function”. More generally, the Clausen function is defined for
complex
(i.e. clsin(2,z)) is the classical
“Clausen function”. More generally, the Clausen function is defined for
complex  and
and  , even when the series does not converge. The
Clausen function is related to the polylogarithm (polylog()) as
, even when the series does not converge. The
Clausen function is related to the polylogarithm (polylog()) as![\mathrm{Cl}_s(z) = \frac{1}{2i}\left(\mathrm{Li}_s\left(e^{iz}\right) -
\mathrm{Li}_s\left(e^{-iz}\right)\right)
= \mathrm{Im}\left[\mathrm{Li}_s(e^{iz})\right] \quad (s, z \in \mathbb{R}),](../_images/math/4393960e5ee6adf31d4e00f2f0c769807e3d224f.png)
and this representation can be taken to provide the analytic continuation of the series. The complementary function clcos() gives the corresponding cosine sum.
Examples
Evaluation for arbitrarily chosen
 and
and  :
:>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> s, z = 3, 4 >>> clsin(s, z); nsum(lambda k: sin(z*k)/k**s, [1,inf]) -0.6533010136329338746275795 -0.6533010136329338746275795
Using
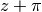 instead of
instead of  gives an alternating series:
gives an alternating series:>>> clsin(s, z+pi) 0.8860032351260589402871624 >>> nsum(lambda k: (-1)**k*sin(z*k)/k**s, [1,inf]) 0.8860032351260589402871624
With
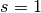 , the sum can be expressed in closed form
using elementary functions:
, the sum can be expressed in closed form
using elementary functions:>>> z = 1 + sqrt(3) >>> clsin(1, z) 0.2047709230104579724675985 >>> chop((log(1-exp(-j*z)) - log(1-exp(j*z)))/(2*j)) 0.2047709230104579724675985 >>> nsum(lambda k: sin(k*z)/k, [1,inf]) 0.2047709230104579724675985
The classical Clausen function
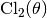 gives the
value of the integral
gives the
value of the integral 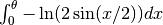 for
for
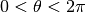 :
:>>> cl2 = lambda t: clsin(2, t) >>> cl2(3.5) -0.2465045302347694216534255 >>> -quad(lambda x: ln(2*sin(0.5*x)), [0, 3.5]) -0.2465045302347694216534255
This function is symmetric about
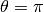 with zeros and extreme
points:
with zeros and extreme
points:>>> cl2(0); cl2(pi/3); chop(cl2(pi)); cl2(5*pi/3); chop(cl2(2*pi)) 0.0 1.014941606409653625021203 0.0 -1.014941606409653625021203 0.0
Catalan’s constant is a special value:
>>> cl2(pi/2) 0.9159655941772190150546035 >>> +catalan 0.9159655941772190150546035
The Clausen sine function can be expressed in closed form when
 is an odd integer (becoming zero when
is an odd integer (becoming zero when  < 0):
< 0):>>> z = 1 + sqrt(2) >>> clsin(1, z); (pi-z)/2 0.3636895456083490948304773 0.3636895456083490948304773 >>> clsin(3, z); pi**2/6*z - pi*z**2/4 + z**3/12 0.5661751584451144991707161 0.5661751584451144991707161 >>> clsin(-1, z) 0.0 >>> clsin(-3, z) 0.0
It can also be expressed in closed form for even integer
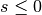 ,
providing a finite sum for series such as
,
providing a finite sum for series such as
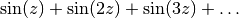 :
:>>> z = 1 + sqrt(2) >>> clsin(0, z) 0.1903105029507513881275865 >>> cot(z/2)/2 0.1903105029507513881275865 >>> clsin(-2, z) -0.1089406163841548817581392 >>> -cot(z/2)*csc(z/2)**2/4 -0.1089406163841548817581392
Call with pi=True to multiply
 by
by 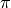 exactly:
exactly:>>> clsin(3, 3*pi) -8.892316224968072424732898e-26 >>> clsin(3, 3, pi=True) 0.0
Evaluation for complex
 ,
,  in a nonconvergent case:
in a nonconvergent case:>>> s, z = -1-j, 1+2j >>> clsin(s, z) (-0.593079480117379002516034 + 0.9038644233367868273362446j) >>> extraprec(20)(nsum)(lambda k: sin(k*z)/k**s, [1,inf]) (-0.593079480117379002516034 + 0.9038644233367868273362446j)
clcos()¶
- mpmath.clcos(s, z)¶
Computes the Clausen cosine function, defined formally by the series
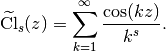
This function is complementary to the Clausen sine function clsin(). In terms of the polylogarithm,
![\mathrm{\widetilde{Cl}}_s(z) =
\frac{1}{2}\left(\mathrm{Li}_s\left(e^{iz}\right) +
\mathrm{Li}_s\left(e^{-iz}\right)\right)
= \mathrm{Re}\left[\mathrm{Li}_s(e^{iz})\right] \quad (s, z \in \mathbb{R}).](../_images/math/78db57c460f9522102ab78cbb7392270629025ea.png)
Examples
Evaluation for arbitrarily chosen
 and
and  :
:>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> s, z = 3, 4 >>> clcos(s, z); nsum(lambda k: cos(z*k)/k**s, [1,inf]) -0.6518926267198991308332759 -0.6518926267198991308332759
Using
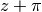 instead of
instead of  gives an alternating series:
gives an alternating series:>>> s, z = 3, 0.5 >>> clcos(s, z+pi) -0.8155530586502260817855618 >>> nsum(lambda k: (-1)**k*cos(z*k)/k**s, [1,inf]) -0.8155530586502260817855618
With
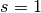 , the sum can be expressed in closed form
using elementary functions:
, the sum can be expressed in closed form
using elementary functions:>>> z = 1 + sqrt(3) >>> clcos(1, z) -0.6720334373369714849797918 >>> chop(-0.5*(log(1-exp(j*z))+log(1-exp(-j*z)))) -0.6720334373369714849797918 >>> -log(abs(2*sin(0.5*z))) # Equivalent to above when z is real -0.6720334373369714849797918 >>> nsum(lambda k: cos(k*z)/k, [1,inf]) -0.6720334373369714849797918
It can also be expressed in closed form when
 is an even integer.
For example,
is an even integer.
For example,>>> clcos(2,z) -0.7805359025135583118863007 >>> pi**2/6 - pi*z/2 + z**2/4 -0.7805359025135583118863007
The case
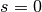 gives the renormalized sum of
gives the renormalized sum of
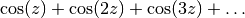 (which happens to be the same for
any value of
(which happens to be the same for
any value of  ):
):>>> clcos(0, z) -0.5 >>> nsum(lambda k: cos(k*z), [1,inf]) -0.5
Also the sums
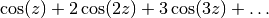
and
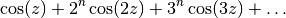
for higher integer powers
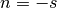 can be done in closed form. They are zero
when
can be done in closed form. They are zero
when  is positive and even (
is positive and even ( negative and even):
negative and even):>>> clcos(-1, z); 1/(2*cos(z)-2) -0.2607829375240542480694126 -0.2607829375240542480694126 >>> clcos(-3, z); (2+cos(z))*csc(z/2)**4/8 0.1472635054979944390848006 0.1472635054979944390848006 >>> clcos(-2, z); clcos(-4, z); clcos(-6, z) 0.0 0.0 0.0
With
 , the series reduces to that of the Riemann zeta function
(more generally, if
, the series reduces to that of the Riemann zeta function
(more generally, if 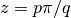 , it is a finite sum over Hurwitz zeta
function values):
, it is a finite sum over Hurwitz zeta
function values):>>> clcos(2.5, 0); zeta(2.5) 1.34148725725091717975677 1.34148725725091717975677 >>> clcos(2.5, pi); -altzeta(2.5) -0.8671998890121841381913472 -0.8671998890121841381913472
Call with pi=True to multiply
 by
by 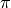 exactly:
exactly:>>> clcos(-3, 2*pi) 2.997921055881167659267063e+102 >>> clcos(-3, 2, pi=True) 0.008333333333333333333333333
Evaluation for complex
 ,
,  in a nonconvergent case:
in a nonconvergent case:>>> s, z = -1-j, 1+2j >>> clcos(s, z) (0.9407430121562251476136807 + 0.715826296033590204557054j) >>> extraprec(20)(nsum)(lambda k: cos(k*z)/k**s, [1,inf]) (0.9407430121562251476136807 + 0.715826296033590204557054j)
polyexp()¶
- mpmath.polyexp(s, z)¶
Evaluates the polyexponential function, defined for arbitrary complex
 ,
,  by the series
by the series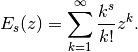
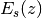 is constructed from the exponential function analogously
to how the polylogarithm is constructed from the ordinary
logarithm; as a function of
is constructed from the exponential function analogously
to how the polylogarithm is constructed from the ordinary
logarithm; as a function of  (with
(with  fixed),
fixed), 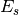 is an L-series
It is an entire function of both
is an L-series
It is an entire function of both  and
and  .
.The polyexponential function provides a generalization of the Bell polynomials
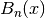 (see bell()) to noninteger orders
(see bell()) to noninteger orders  .
In terms of the Bell polynomials,
.
In terms of the Bell polynomials,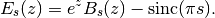
Note that
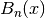 and
and 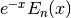 are identical if
are identical if  is a nonzero integer, but not otherwise. In particular, they differ
at
is a nonzero integer, but not otherwise. In particular, they differ
at 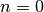 .
.Examples
Evaluating a series:
>>> from mpmath import * >>> mp.dps = 25; mp.pretty = True >>> nsum(lambda k: sqrt(k)/fac(k), [1,inf]) 2.101755547733791780315904 >>> polyexp(0.5,1) 2.101755547733791780315904
Evaluation for arbitrary arguments:
>>> polyexp(-3-4j, 2.5+2j) (2.351660261190434618268706 + 1.202966666673054671364215j)
Evaluation is accurate for tiny function values:
>>> polyexp(4, -100) 3.499471750566824369520223e-36
If
 is a nonpositive integer,
is a nonpositive integer, 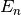 reduces to a special
instance of the hypergeometric function
reduces to a special
instance of the hypergeometric function 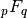 :
:>>> n = 3 >>> x = pi >>> polyexp(-n,x) 4.042192318847986561771779 >>> x*hyper([1]*(n+1), [2]*(n+1), x) 4.042192318847986561771779
Zeta function variants¶
primezeta()¶
- mpmath.primezeta(s)¶
Computes the prime zeta function, which is defined in analogy with the Riemann zeta function (zeta()) as
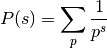
where the sum is taken over all prime numbers
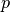 . Although
this sum only converges for
. Although
this sum only converges for 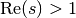 , the
function is defined by analytic continuation in the
half-plane
, the
function is defined by analytic continuation in the
half-plane 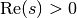 .
.Examples
Arbitrary-precision evaluation for real and complex arguments is supported:
>>> from mpmath import * >>> mp.dps = 30; mp.pretty = True >>> primezeta(2) 0.452247420041065498506543364832 >>> primezeta(pi) 0.15483752698840284272036497397 >>> mp.dps = 50 >>> primezeta(3) 0.17476263929944353642311331466570670097541212192615 >>> mp.dps = 20 >>> primezeta(3+4j) (-0.12085382601645763295 - 0.013370403397787023602j)
The prime zeta function has a logarithmic pole at
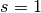 ,
with residue equal to the difference of the Mertens and
Euler constants:
,
with residue equal to the difference of the Mertens and
Euler constants:>>> primezeta(1) +inf >>> extradps(25)(lambda x: primezeta(1+x)+log(x))(+eps) -0.31571845205389007685 >>> mertens-euler -0.31571845205389007685
The analytic continuation to
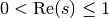 is implemented. In this strip the function exhibits
very complex behavior; on the unit interval, it has poles at
is implemented. In this strip the function exhibits
very complex behavior; on the unit interval, it has poles at
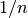 for every squarefree integer
for every squarefree integer  :
:>>> primezeta(0.5) # Pole at s = 1/2 (-inf + 3.1415926535897932385j) >>> primezeta(0.25) (-1.0416106801757269036 + 0.52359877559829887308j) >>> primezeta(0.5+10j) (0.54892423556409790529 + 0.45626803423487934264j)
Although evaluation works in principle for any
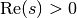 ,
it should be noted that the evaluation time increases exponentially
as
,
it should be noted that the evaluation time increases exponentially
as  approaches the imaginary axis.
approaches the imaginary axis.For large
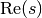 ,
, 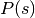 is asymptotic to
is asymptotic to 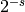 :
:>>> primezeta(inf) 0.0 >>> primezeta(10), mpf(2)**-10 (0.00099360357443698021786, 0.0009765625) >>> primezeta(1000) 9.3326361850321887899e-302 >>> primezeta(1000+1000j) (-3.8565440833654995949e-302 - 8.4985390447553234305e-302j)
References
Carl-Erik Froberg, “On the prime zeta function”, BIT 8 (1968), pp. 187-202.
secondzeta()¶
- mpmath.secondzeta(s, a=0.015, **kwargs)¶
Evaluates the secondary zeta function
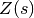 , defined for
, defined for
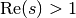 by
by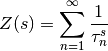
where
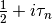 runs through the zeros of
runs through the zeros of 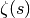 with
imaginary part positive.
with
imaginary part positive.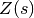 extends to a meromorphic function on
extends to a meromorphic function on 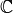 with a
double pole at
with a
double pole at 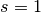 and simple poles at the points
and simple poles at the points 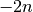 for
for
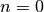 , 1, 2, ...
, 1, 2, ...Examples
>>> from mpmath import * >>> mp.pretty = True; mp.dps = 15 >>> secondzeta(2) 0.023104993115419 >>> xi = lambda s: 0.5*s*(s-1)*pi**(-0.5*s)*gamma(0.5*s)*zeta(s) >>> Xi = lambda t: xi(0.5+t*j) >>> -0.5*diff(Xi,0,n=2)/Xi(0) (0.023104993115419 + 0.0j)
We may ask for an approximate error value:
>>> secondzeta(0.5+100j, error=True) ((-0.216272011276718 - 0.844952708937228j), 2.22044604925031e-16)
The function has poles at the negative odd integers, and dyadic rational values at the negative even integers:
>>> mp.dps = 30 >>> secondzeta(-8) -0.67236328125 >>> secondzeta(-7) +inf
Implementation notes
The function is computed as sum of four terms
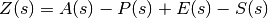 respectively main, prime, exponential and singular terms.
The main term
respectively main, prime, exponential and singular terms.
The main term 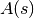 is computed from the zeros of zeta.
The prime term depends on the von Mangoldt function.
The singular term is responsible for the poles of the function.
is computed from the zeros of zeta.
The prime term depends on the von Mangoldt function.
The singular term is responsible for the poles of the function.The four terms depends on a small parameter
 . We may change the
value of
. We may change the
value of  . Theoretically this has no effect on the sum of the four
terms, but in practice may be important.
. Theoretically this has no effect on the sum of the four
terms, but in practice may be important.A smaller value of the parameter
 makes
makes 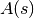 depend on
a smaller number of zeros of zeta, but
depend on
a smaller number of zeros of zeta, but 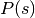 uses more values of
von Mangoldt function.
uses more values of
von Mangoldt function.We may also add a verbose option to obtain data about the values of the four terms.
>>> mp.dps = 10 >>> secondzeta(0.5 + 40j, error=True, verbose=True) main term = (-30190318549.138656312556 - 13964804384.624622876523j) computed using 19 zeros of zeta prime term = (132717176.89212754625045 + 188980555.17563978290601j) computed using 9 values of the von Mangoldt function exponential term = (542447428666.07179812536 + 362434922978.80192435203j) singular term = (512124392939.98154322355 + 348281138038.65531023921j) ((0.059471043 + 0.3463514534j), 1.455191523e-11)
>>> secondzeta(0.5 + 40j, a=0.04, error=True, verbose=True) main term = (-151962888.19606243907725 - 217930683.90210294051982j) computed using 9 zeros of zeta prime term = (2476659342.3038722372461 + 28711581821.921627163136j) computed using 37 values of the von Mangoldt function exponential term = (178506047114.7838188264 + 819674143244.45677330576j) singular term = (175877424884.22441310708 + 790744630738.28669174871j) ((0.059471043 + 0.3463514534j), 1.455191523e-11)
Notice the great cancellation between the four terms. Changing
 , the
four terms are very different numbers but the cancellation gives
the good value of Z(s).
, the
four terms are very different numbers but the cancellation gives
the good value of Z(s).References
A. Voros, Zeta functions for the Riemann zeros, Ann. Institute Fourier, 53, (2003) 665–699.
A. Voros, Zeta functions over Zeros of Zeta Functions, Lecture Notes of the Unione Matematica Italiana, Springer, 2009.